题目内容
三棱锥P-ABC中,PA、PB、PC两两垂直且PA=2
,PB=4,PC=2
,如果三棱锥的四个顶点都在同一球面上,那么这个球的体积等于( )
| 2 |
| 3 |
| A、36π | B、72π |
| C、144π | D、288π |
考点:球的体积和表面积
专题:球
分析:根据题意,以PA、PB、PC为长方体的长、宽、高,作长方体PABD-CEFG,连结BE、PE.可得三棱锥P-ABC的外接球就是长方体PABD-CEFG的外接球,球心是长方体的对角线的中点O,求出半径即可求解外接球的体积.
解答:
解: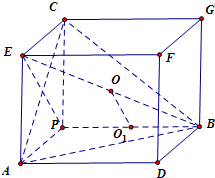 以PA、PB、PC为长方体的长、宽、高,作长方体PABD-CEFG
以PA、PB、PC为长方体的长、宽、高,作长方体PABD-CEFG
如图所示,连结BE、PE
∵三棱锥P-ABC的四个顶点都在同一球面上,
∴长方体PABD-CEFG的外接球与三棱锥P-ABC的外接球是同一个球
可得球心为长方体对角线BE的中点,球的直径为长方体对角线长,
设O为BE中点,则O为三棱锥P-ABC的外接球心,
根据球的性质,可得OE=
=
=3.
球的体积:
πR3=36π,
故选:A.
 以PA、PB、PC为长方体的长、宽、高,作长方体PABD-CEFG
以PA、PB、PC为长方体的长、宽、高,作长方体PABD-CEFG如图所示,连结BE、PE
∵三棱锥P-ABC的四个顶点都在同一球面上,
∴长方体PABD-CEFG的外接球与三棱锥P-ABC的外接球是同一个球
可得球心为长方体对角线BE的中点,球的直径为长方体对角线长,
设O为BE中点,则O为三棱锥P-ABC的外接球心,
根据球的性质,可得OE=
| 1 |
| 2 |
| PA2+PB2+PC2 |
| 1 |
| 2 |
| 8+16+12 |
球的体积:
| 4 |
| 3 |
故选:A.
点评:本题给出三棱锥的外接球,求它的外接球心到直线PB的距离.着重考查了球的性质、长方体的外接球、三角形中位线定理和勾股定理等知识,属于中档.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的表面积为( )
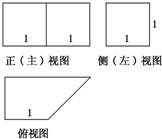

A、6+
| ||
B、7+
| ||
C、8+
| ||
D、7+2
|
已知i是虚数单位,复数z满足:(1-2i)z=(1+i)2,则z的值是( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
函数f(x)=2
sinxcosx+
cos2x的最小正周期和振幅分别是( )
| 6 |
| 2 |
A、π,
| ||
B、π,
| ||
| C、2π,1 | ||
D、π,2
|
已知a、b为直线,α为平面,则下面四个命题:
①若a∥b,a⊥α,则b⊥α;
②若a⊥α,b⊥α,则a∥b;
③若a⊥α,a⊥b,则b∥α;
④若a∥α,a⊥b,则b⊥α;
其中正确的命题是( )
①若a∥b,a⊥α,则b⊥α;
②若a⊥α,b⊥α,则a∥b;
③若a⊥α,a⊥b,则b∥α;
④若a∥α,a⊥b,则b⊥α;
其中正确的命题是( )
| A、①② | B、①②③ |
| C、②③④ | D、①②④ |
已知点O(0,0),A(1,2),B(3,2),以线段AB为直径作圆C,则直线l:x+y-3=0与圆C的位置关系是( )
| A、相交且过圆心 | B、相交但不过圆心 |
| C、相切 | D、相离 |
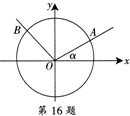 如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A (x1,yl),将射线OA按逆时针方向旋转
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A (x1,yl),将射线OA按逆时针方向旋转