题目内容
已知集合A={x|-3<x<4},集合B={x|x2+2x-8>0},集合C={x|x2-4ax+3a2<0,a≠0},
(Ⅰ)求A∩(∁RB);
(Ⅱ)若C⊆A,试确定实数a的取值范围?
(Ⅰ)求A∩(∁RB);
(Ⅱ)若C⊆A,试确定实数a的取值范围?
考点:交、并、补集的混合运算
专题:集合
分析:(Ⅰ)求出B中不等式的解集确定出B,根据全集R求出B的补集,求出A与B补集的交集即可;
(Ⅱ)根据a大于0与a小于0分别求出C中不等式的解集,根据C为A的子集即可确定出a的范围.
(Ⅱ)根据a大于0与a小于0分别求出C中不等式的解集,根据C为A的子集即可确定出a的范围.
解答:
解:(Ⅰ)由B中不等式变形得:(x-2)(x+4)>0,
解得:x<-4或x>2,即B={x|x<-4或x>2},
∵全集为R,
∴∁RB={x|-4≤x≤2},
∵A={x|-3<x<4},
∴A∩(∁RB)={x|-3<x≤2};
(Ⅱ)由C中不等式变形得:(x-a)(x-3a)<0,
分两种情况考虑:
当a>0时,C=(a,3a),
∵C⊆A,
∴
,
解得:-3≤a≤
,
此时a的范围为0<a≤
;
当a<0时,C=(3a,a),
∵C⊆A,
∴
,
解得:-1≤a≤4,
此时a的范围为-1≤a<0,
综上,a的取值范围是-1≤a<0或0<a≤
.
解得:x<-4或x>2,即B={x|x<-4或x>2},
∵全集为R,
∴∁RB={x|-4≤x≤2},
∵A={x|-3<x<4},
∴A∩(∁RB)={x|-3<x≤2};
(Ⅱ)由C中不等式变形得:(x-a)(x-3a)<0,
分两种情况考虑:
当a>0时,C=(a,3a),
∵C⊆A,
∴
|
解得:-3≤a≤
| 4 |
| 3 |
此时a的范围为0<a≤
| 4 |
| 3 |
当a<0时,C=(3a,a),
∵C⊆A,
∴
|
解得:-1≤a≤4,
此时a的范围为-1≤a<0,
综上,a的取值范围是-1≤a<0或0<a≤
| 4 |
| 3 |
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
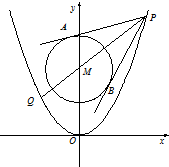 已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为
已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为