题目内容
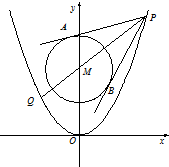 已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为
已知抛物线C1:x2=2py(p>0),圆C2:x2+y2-8y+12=0的圆心M到抛物线C1的准线的距离为| 9 |
| 2 |
(Ⅰ)求抛物线C1的方程;
(Ⅱ)求直线PQ的方程及
| PA |
| PB |
考点:抛物线的标准方程,平面向量数量积的运算
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由已知条件推导出4+
=
,由此能求出抛物线C1的方程.
(Ⅱ)设PQ的方程:y=kx+4,由
,得x2-2kx-8=0,由此利用韦达定理结合已知条件能求出直线PQ的方程及
•
的值.
| p |
| 2 |
| 9 |
| 2 |
(Ⅱ)设PQ的方程:y=kx+4,由
|
| PA |
| PB |
解答:
 (本小题满分13分)
(本小题满分13分)
解:(Ⅰ)C2:x2+(y-4)2=4,∴M(0,4),…(1分)
抛物线C1:x2=2py的准线方程是y=-
,
依题意:4+
=
,∴p=1,…(3分)
∴抛物线C1的方程为:x2=2y.…(4分)
(Ⅱ)设PQ的方程:y=kx+4,
由
,得x2-2kx-8=0,设P(x1,y1),Q(x2,y2),
则
=(-x1,4-y1),
=(x2,y2-4),
∵|PM|=2|MQ|,∴
=2
,∴-x1=2x2,…①
又x1+x2=2k,…②,x1x2=-8,…③,
由①②③得k=±1,
∴PQ的方程为:y=±x+4.…(9分)
取PQ的方程:y=x+4,和抛物线x2=2y,联立得P点坐标为P(4,8)
∴|
|=4
,连接AM,BM,|
|=|
|=
=2
,
设∠APM=α,则sinα=
=
=
,…(11分)
∴
•
=|
|•|
|cos2α
=28(1-2sin2α)=21.…(13分)
 (本小题满分13分)
(本小题满分13分)解:(Ⅰ)C2:x2+(y-4)2=4,∴M(0,4),…(1分)
抛物线C1:x2=2py的准线方程是y=-
| p |
| 2 |
依题意:4+
| p |
| 2 |
| 9 |
| 2 |
∴抛物线C1的方程为:x2=2y.…(4分)
(Ⅱ)设PQ的方程:y=kx+4,
由
|
则
| PM |
| MQ |
∵|PM|=2|MQ|,∴
| PM |
| MQ |
又x1+x2=2k,…②,x1x2=-8,…③,
由①②③得k=±1,
∴PQ的方程为:y=±x+4.…(9分)
取PQ的方程:y=x+4,和抛物线x2=2y,联立得P点坐标为P(4,8)
∴|
| PM |
| 2 |
| PA |
| PB |
| PM2-PA2 |
| 7 |
设∠APM=α,则sinα=
| AM |
| PM |
| 2 | ||
4
|
| ||
| 4 |
∴
| PA |
| PB |
| PA |
| PB |
=28(1-2sin2α)=21.…(13分)
点评:本题考查抛物线方程的求法,考查直线方程的求法,考查向量的数量积的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了解甲、乙两批次产品中某微量元素的含量,采用随机抽样的方法从两批次产品中各抽取4件,测得它们所含微量元素(单位:毫克)如表:
根据抽样数据推测( )
| 产品编号 | 1 | 2 | 3 | 4 |
| 甲批产品所含微量元素x | 890 | 890 | 850 | 950 |
| 乙批产品所含微量元素y | 900 | 850 | 910 | 920 |
| A、甲批产品所含微量元素比较稳定 |
| B、乙批产品所含微量元素比较稳定 |
| C、两批产品所含微量元素一样稳定 |
| D、以上判断都不对 |
