题目内容
(Ⅰ)已知0<θ<π,sinθ+cosθ=
,求cos2θ的值;
(Ⅱ)已知-
<α<0<β<
,cos(α-β)=
,sinβ=
,求tanα的值.
| 1 |
| 3 |
(Ⅱ)已知-
| π |
| 2 |
| π |
| 2 |
| 3 |
| 5 |
| 5 |
| 13 |
考点:二倍角的余弦
专题:三角函数的求值
分析:(Ⅰ)吧所给的等式平方可得sin2θ=-
<0,可得θ∈(
,
),2θ∈(π,
),cos2θ<0.再根据
cos2θ=-
,计算求得结果.
(Ⅱ)由条件利用同角三角函数的基本关系求得tanβ 和tan(α-β)的值,再根据tanα=tan[(α-β)+β],利用两角和的正切公式计算求得结果.
| 8 |
| 9 |
| π |
| 2 |
| 3π |
| 4 |
| 3π |
| 2 |
cos2θ=-
| 1-sin22θ |
(Ⅱ)由条件利用同角三角函数的基本关系求得tanβ 和tan(α-β)的值,再根据tanα=tan[(α-β)+β],利用两角和的正切公式计算求得结果.
解答:
解:(Ⅰ)∵已知0<θ<π,sinθ+cosθ=
,平方可得 1+2sinθcosθ=
,
∴sin2θ=-
<0,∴θ∈(
,π),sinθ>0,cosθ<0,|sinθ|>|cosθ|,
∴θ∈(
,
),∴2θ∈(π,
),∴cos2θ<0.
∴cos2θ=-
=-
=-
.
(Ⅱ)∵已知-
<α<0<β<
,sinβ=
,
∴cosβ=
=
,∴tanβ=
=
.
∵cos(α-β)=
,∴-
<α-β<0,∴sin(α-β)=-
=-
,tan(α-β)=-
.
∴tanα=tan[(α-β)+β]=
=
=-
.
| 1 |
| 3 |
| 1 |
| 9 |
∴sin2θ=-
| 8 |
| 9 |
| π |
| 2 |
∴θ∈(
| π |
| 2 |
| 3π |
| 4 |
| 3π |
| 2 |
∴cos2θ=-
| 1-sin22θ |
1-
|
| ||
| 9 |
(Ⅱ)∵已知-
| π |
| 2 |
| π |
| 2 |
| 5 |
| 13 |
∴cosβ=
| 1-sin2β |
| 12 |
| 13 |
| sinβ |
| cosβ |
| 5 |
| 12 |
∵cos(α-β)=
| 3 |
| 5 |
| π |
| 2 |
| 1-cos2(α-β) |
| 4 |
| 5 |
| 4 |
| 3 |
∴tanα=tan[(α-β)+β]=
| tan(α-β)+tanβ |
| 1-tan(α-β)tanβ |
-
| ||||
1-(
|
| 33 |
| 56 |
点评:本题主要考查同角三角函数的基本关系、二倍角公式、两角和差的三角公式的应用,属于基础题.

练习册系列答案
相关题目
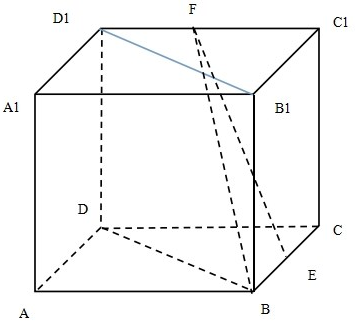 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是棱BC、C1D1的中点.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是棱BC、C1D1的中点.