题目内容
计算:cos
π•cos
π•cos
π的值.
| 2 |
| 7 |
| 4 |
| 7 |
| 6 |
| 7 |
考点:二倍角的正弦,运用诱导公式化简求值
专题:三角函数的求值
分析:利用诱导公式以及二倍角的正弦函数,化简求解即可.
解答:
解:cos
π•cos
π•cos
π
=-cos
π•cos
π•cos
π
=-
=-
=-
=-
=
=
.
| 2 |
| 7 |
| 4 |
| 7 |
| 6 |
| 7 |
=-cos
| 1 |
| 7 |
| 2 |
| 7 |
| 4 |
| 7 |
=-
8sin
| ||||||||
8sin
|
=-
4sin
| ||||||
8sin
|
=-
2sin
| ||||
8sin
|
=-
sin
| ||
8sin
|
=
sin
| ||
8sin
|
=
| 1 |
| 8 |
点评:本题考查三角函数的化简求值,注意函数的表达式的分析,发现表达式都是余弦函数,而且角是二倍角关系,是解题的关键.

练习册系列答案
相关题目
已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2,3),求过两点A(a1,b1)、B(a2,b2)(a1≠a2)的直线方程( )
| A、3x+2y+1=0 |
| B、5x+y+1=0 |
| C、x+5y+1=0 |
| D、2x+3y+1=0 |
已知集合A={x|y=
},B={y|y=3x,x<0},则A∩B=( )
| log3x+1 |
A、(
| ||
B、[
| ||
C、(0,
| ||
D、[
|
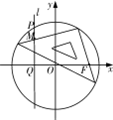 如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且
如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且