题目内容
正四棱柱ABCD-A′B′C′D′中，底面边长为1，侧棱长为2，且MN是AB′，BC′的公垂线，M在AB′上，N在BC′上，则线段MN的长度为 ．
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：以D为原点，建立空间直角坐标系D-xyz，利用向量法能求出MN的长．
解答：
解：以D为原点，建立空间直角坐标系D-xyz，
则A（1，0，0），B′（1，0，2），
B（1，1，0），C′（0，1，2），
=（0，1，2），
=（-1，0，2），
=（0，1，0），
设异面直线AB′，BC′的公共法向量
=（x，y，z），
则
，
取x=2，得
=（2，-2，1），
∴线段MN的长度d=
=
=
．
故答案为：
．
解：以D为原点，建立空间直角坐标系D-xyz，则A（1，0，0），B′（1，0，2），
B（1，1，0），C′（0，1，2），
| AB′ |
| BC′ |
| AB |
设异面直线AB′，BC′的公共法向量
| n |
则
|
取x=2，得
| n |
∴线段MN的长度d=
|
| ||||
|
|
| |-2| |
| 3 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查两条异面直线的公垂线段的长的求法，是中档题，解题时要注意向量法的合理运用．
练习册系列答案
相关题目
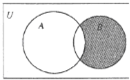设区间U={1，2，3，4，5，6，7，8，9}，集合A={1，2，3，5}，B={2，4，6，7}，则图中的阴影部分表示的集合为（ ）| A、{2} |
| B、{4，6，7} |
| C、{1，2，5} |
| D、{4，6，7，8} |
下列选项的对象中能构成集合的为（ ）
| A、一切很大的数 |
| B、聪明人 |
| C、正三角形的全体 |
| D、高一教材中的所有难题 |
已知集合A={x|x-2=0}，B={0，1，2}，则A∩B=（ ）
| A、{0} | B、{0，1，} |
| C、{2} | D、{0，1，2} |
已知正三棱锥P-ABC中，PA=PB=PC=1，且PA，PB，PC两两垂直，则该三棱锥外接球的表面积为（ ）
A、
| ||
B、
| ||
| C、3π | ||
| D、12π |