题目内容
已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2,3),求过两点A(a1,b1)、B(a2,b2)(a1≠a2)的直线方程( )
| A、3x+2y+1=0 |
| B、5x+y+1=0 |
| C、x+5y+1=0 |
| D、2x+3y+1=0 |
考点:两条直线的交点坐标
专题:直线与圆
分析:把P点坐标代入两直线a1x+b1y+1=0和a2x+b2y+1=0,求出过两点A(a1,b1)、B(a2,b2)的斜率,再求过两点A(a1,b1)、B(a2,b2)(a1≠a2)的直线方程.
解答:
解:∵两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2,3),
∴2a1+3b1+1=0,2a2+3b2+1=0,
∴2(a1-a2)+3(b1-b2)=0,即
=-
.
∴所求直线方程为y-b1=-
(x-a1).
∴2x+3y-(2a1+3b1)=0,
即2x+3y+1=0.
故选:D.
∴2a1+3b1+1=0,2a2+3b2+1=0,
∴2(a1-a2)+3(b1-b2)=0,即
| b1-b2 |
| a1-a2 |
| 2 |
| 3 |
∴所求直线方程为y-b1=-
| 2 |
| 3 |
∴2x+3y-(2a1+3b1)=0,
即2x+3y+1=0.
故选:D.
点评:本题考查了两直线的交点坐标,考查了直线方程的求法,是中档题.

练习册系列答案
相关题目
等差数列{an}的公差d<0,且a12=a20142,若数列{an}的前n项和Sn最大,Sm=0,则m-n的值为( )
| A、1007 | B、1006 |
| C、1005 | D、1004 |
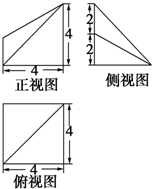 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
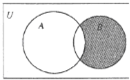 设区间U={1,2,3,4,5,6,7,8,9},集合A={1,2,3,5},B={2,4,6,7},则图中的阴影部分表示的集合为( )
设区间U={1,2,3,4,5,6,7,8,9},集合A={1,2,3,5},B={2,4,6,7},则图中的阴影部分表示的集合为( )| A、{2} |
| B、{4,6,7} |
| C、{1,2,5} |
| D、{4,6,7,8} |
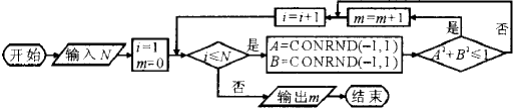
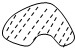 如图,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为
如图,边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为