题目内容
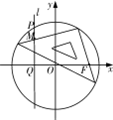 如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且
如图,设P是圆O:x2+y2=2上的点,过P作直线l垂直x轴于点Q,M为l上一点,且| PQ |
| 2 |
| MQ |
(1)求曲线P的方程;
(2)某同学研究发现:若把三角形的直角顶点放置在圆O的圆周上,使其一条直角边过点F(1,0),则三角板的另一条直角边所在直线与曲线P有且只有一个公共点.你认为该同学的结论是否正确?若正确,请证明;若不正确,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设M(x,y),P(x0,y0),xP=x.yP=
y,由已知得x2+(
y)2=2,由此能求出曲线P的方程.(2)设三角板的直角顶点放置在圆O的圆周上的点N(a,b)处,则a2+b2=2,又设三角板的另一版权法直角边所在直线为l′,由此根据a的取值范围进行分类讨论,能求出l′与曲线P有且只有一个公共点,该同学的结论正确.
| 2 |
| 2 |
解答:
解:(1)设M(x,y),P(x0,y0),
∵PQ⊥x轴于点Q,M为直线l上一点,且PQ=
MQ,
∴xP=x.yP=
y,
∵点P在圆O:x2+y2=2上,∴xP2+yp2=2,
∴x2+(
y)2=2,整理,得
+y2=1,
∴曲线P的方程为
+y2=1.
(2)设三角板的直角顶点放置在圆O的圆周上的点N(a,b)处,
则a2+b2=2,
又设三角板的另一版权法直角边所在直线为l′,
(i)当a=1时,直线NF⊥x轴,l′:y=±1,
由题意知l′与曲线P有且只有一个公共点.
(ii)当a≠1时,则kNP=
,
若b=0,则直线l′:x=±
,由题意知l′与曲线P有且只有一个公共点,
若b≠0,则直线l′的斜率k=
,
∴l′:y-b=
(x-a),即y=
x+
,
由
,得[b2+2(1-a2)]x2+4(1-a)(2-a)x+2[(2-a2)-b2]=0,(*)
又b2=2-a2,
∴方程(*)可化为(a-2)2x2+4(1-a)(2-a)x+4(a-1)2=0,
∴△=[4(1-a)(1-2a)]2-16(a-2)2(a-1)2=0,
∴l′与曲线P有且只有一个公共点
综上所述,该同学的结论正确.
∵PQ⊥x轴于点Q,M为直线l上一点,且PQ=
| 2 |

∴xP=x.yP=
| 2 |
∵点P在圆O:x2+y2=2上,∴xP2+yp2=2,
∴x2+(
| 2 |
| x2 |
| 2 |
∴曲线P的方程为
| x2 |
| 2 |
(2)设三角板的直角顶点放置在圆O的圆周上的点N(a,b)处,
则a2+b2=2,
又设三角板的另一版权法直角边所在直线为l′,
(i)当a=1时,直线NF⊥x轴,l′:y=±1,
由题意知l′与曲线P有且只有一个公共点.
(ii)当a≠1时,则kNP=
| b |
| a-1 |
若b=0,则直线l′:x=±
| 2 |
若b≠0,则直线l′的斜率k=
| 1-a |
| b |
∴l′:y-b=
| 1-a |
| b |
| 1-a |
| b |
| 2-a |
| b |
由
|
又b2=2-a2,
∴方程(*)可化为(a-2)2x2+4(1-a)(2-a)x+4(a-1)2=0,
∴△=[4(1-a)(1-2a)]2-16(a-2)2(a-1)2=0,
∴l′与曲线P有且只有一个公共点
综上所述,该同学的结论正确.
点评:本题考查圆的方程与性质、椭圆的标准方程与性质、直线与圆锥曲线的关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、特殊与一般思想.

练习册系列答案
相关题目
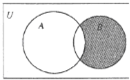 设区间U={1,2,3,4,5,6,7,8,9},集合A={1,2,3,5},B={2,4,6,7},则图中的阴影部分表示的集合为( )
设区间U={1,2,3,4,5,6,7,8,9},集合A={1,2,3,5},B={2,4,6,7},则图中的阴影部分表示的集合为( )| A、{2} |
| B、{4,6,7} |
| C、{1,2,5} |
| D、{4,6,7,8} |
已知正三棱锥P-ABC中,PA=PB=PC=1,且PA,PB,PC两两垂直,则该三棱锥外接球的表面积为( )
A、
| ||
B、
| ||
| C、3π | ||
| D、12π |