题目内容
如图1,⊙O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=
,∠DBA=
,沿直径AB折起,使两个半圆所在平面互相垂直(如图2),E为AO的中点.
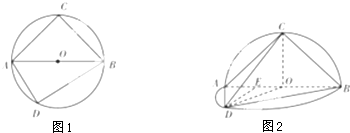
(1)求证:CB⊥DE;
(2)求三棱锥C-BOD的体积;
(3)求二角C-BD-O的正切值.
| π |
| 4 |
| π |
| 6 |

(1)求证:CB⊥DE;
(2)求三棱锥C-BOD的体积;
(3)求二角C-BD-O的正切值.
考点:棱柱、棱锥、棱台的体积,二面角的平面角及求法
专题:空间位置关系与距离
分析:(1)利用等边三角形的性质可得DE⊥AO,再利用面面垂直的性质定理即可得到DE⊥平面ABC,进而得出结果.
(2)Rt△ADB中,AB=2,AD=1,O到DB的距离为OF=
,△OBD的面积为
×
×
=
,求解体积即可.
(3)确定∠CFO为二角C-BD-O的平面角,运用直角三角形求解即可.
(2)Rt△ADB中,AB=2,AD=1,O到DB的距离为OF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
(3)确定∠CFO为二角C-BD-O的平面角,运用直角三角形求解即可.
解答:
(Ⅰ)证明:在△AOD中,∠DBA=
,
∵∠OAD=
,OA=OD,
∴△AOD为正三角形,
又∵E为OA的中点,
∴DE⊥AO,
∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,
∴DE⊥平面ABC.
又CB?平面ABC,
∴CB⊥DE.
(2)∵⊙O的直径AB=2,∠CAB=
,
∴OC⊥AB,OC=2,OC⊥平面ADB,
∵∠DBA=
,

∴Rt△ADB中,AB=2,AD=1,O到DB的距离为OF=
,
∴△OBD的面积为
×
×
=
,
∴三棱锥C-BOD的体积=
×
×2=
,
(3)∵OC⊥平面ADB,OF⊥BD,
∴BD⊥面COF,
∴BD⊥CF,
∴∠CFO为二角C-BD-O的平面角.
∴tan∠CFO=
=
=4
故二角C-BD-O的正切值为4.
| π |
| 6 |
∵∠OAD=
| π |
| 3 |
∴△AOD为正三角形,
又∵E为OA的中点,
∴DE⊥AO,
∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,
∴DE⊥平面ABC.
又CB?平面ABC,
∴CB⊥DE.
(2)∵⊙O的直径AB=2,∠CAB=
| π |
| 4 |
∴OC⊥AB,OC=2,OC⊥平面ADB,
∵∠DBA=
| π |
| 6 |

∴Rt△ADB中,AB=2,AD=1,O到DB的距离为OF=
| 1 |
| 2 |
∴△OBD的面积为
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
∴三棱锥C-BOD的体积=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 6 |
(3)∵OC⊥平面ADB,OF⊥BD,
∴BD⊥面COF,
∴BD⊥CF,
∴∠CFO为二角C-BD-O的平面角.
∴tan∠CFO=
| OC |
| OF |
| 2 | ||
|
故二角C-BD-O的正切值为4.
点评:本题考查了空间平面中的图形的性质,折叠图形,求解面积,体积问题,夹角,垂直常见的问题,注意线段的长度求解看两个图形的求解即可.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
下列选项的对象中能构成集合的为( )
| A、一切很大的数 |
| B、聪明人 |
| C、正三角形的全体 |
| D、高一教材中的所有难题 |