题目内容
已知集合A={x|y=
}，B={y|y=3x，x＜0}，则A∩B=（ ）
| log3x+1 |
A、(
| ||
B、[
| ||
C、(0，
| ||
D、[
|
考点：交集及其运算
专题：函数的性质及应用,集合
分析：由对数函数、指数函数的性质求出集合A、B，再由交集的运算求出A∩B．
解答：
解：由
+1≥0得，
≥-1
，
解得x≥
，所以集合A=[
，+∞），
因为y=3x，x＜0，所以0＜y＜1，则集合B=（0，1），
所以A∩B=[
，1），
故选：D．
| log | x 3 |
| log | x 3 |
| =log |
3 |
解得x≥
| 1 |
| 3 |
| 1 |
| 3 |
因为y=3x，x＜0，所以0＜y＜1，则集合B=（0，1），
所以A∩B=[
| 1 |
| 3 |
故选：D．
点评：本题考查交集及其运算，以及对数函数、指数函数的性质，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
等差数列{an}的公差d＜0，且a12=a20142，若数列{an}的前n项和Sn最大，Sm=0，则m-n的值为（ ）
| A、1007 | B、1006 |
| C、1005 | D、1004 |
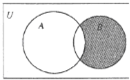设区间U={1，2，3，4，5，6，7，8，9}，集合A={1，2，3，5}，B={2，4，6，7}，则图中的阴影部分表示的集合为（ ）| A、{2} |
| B、{4，6，7} |
| C、{1，2，5} |
| D、{4，6，7，8} |
正弦定理是指（ ）
| A、a=sinA | ||||||
| B、b=sinB | ||||||
| C、c=sinC | ||||||
D、
|
下列选项的对象中能构成集合的为（ ）
| A、一切很大的数 |
| B、聪明人 |
| C、正三角形的全体 |
| D、高一教材中的所有难题 |