题目内容
3.已知函数f(x)的定义域为R,对任意实数x,y满足f (x+y)=f(x)+f (y)+0.5,且f (0.5)=0,当x>0.5时,f(x)>0,给出以下结论:①f (0)=-0.5;
②f (-1)=-1.5;
③f(x)为R上的减函数;
④f(x)+0.5为奇函数;
⑤f(x)+1为偶函数.
其中正确结论的序号是①②④.
分析 ①,由题意和x,y的任意性,取x=y=0代入可得f(0);
②,取x=0.5,y=-0.5,可得f(-0.5),取x=y=-0.5代入可得f(-1);
③,由①②知f(0)>f(-1),f(x)不为R上的减函数,;
④,令y=-x代入可得f(x)+0.5+f(-x)+0.5=0;
⑤,f(0.5)+1≠f(-0.5)+1,可得f(x)+1不为偶函数;
解答 解:对于①,由题意和x,y的任意性,取x=y=0代入可得f(0)=f(0)+f(0)+0.5,f(0)=-0.5故①正确;
对于②,取x=0.5,y=-0.5,可得f(0)=f(0.5)+f(-0.5)+0.5⇒f(-0.5)=-1,取x=y=-0.5代入可得f(-1)=f(-0.5)+f(-0.5)+0.5=-1.5,故②正确;
对于③,由①②知f(0)>f(-1),∴f(x)不为R上的减函数,故③错;
对于④,令y=-x代入可得f(0)=f(x)+f(-x)+0.5⇒f(x)+0.5+f(-x)+0.5=0,即 f(x)+0.5为奇函数,故④正确;
对于⑤,f(0.5)+1=1,f(-0.5)+1=0,∴f(x)+1=f(-x)+1不恒成立,f(x)+1不为偶函数,故⑤错;
故答案为:①②④
点评 本题考查命题真假的判断,赋值法、函数的性质是解题关键,属中档题.

练习册系列答案
相关题目
13.已知函数f(x)的定义域为R,且x3f(x)+x3f(-x)=0,若对任意x∈[0,+∞)都有3xf(x)+x2f'(x)<2,则不等式x3f(x)-8f(2)<x2-4的解集为( )
| A. | (-2,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-4,4) | D. | (-∞,-4)∪(4,+∞) |
14.三棱锥的棱长均为4$\sqrt{6}$,顶点在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 144π | D. | 288π |
18.如图,PA垂直于矩形ABCD所在的平面,则图中与平面PCD垂直的平面是( )
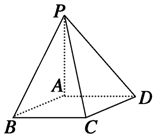

| A. | 平面ABCD | B. | 平面PBC | C. | 平面PAD | D. | 平面PBC |
8.已知a=2${\;}^{\frac{1}{3}}$,b=log3$\frac{1}{2}$,c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,则( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
15.已知(1,1)是直线l被椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{9}$=1所截得的线段的中点,则l的斜率是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{4}$ | D. | $\frac{1}{4}$ |
12.已知集合A={x|y=x2},集合B={y|y=x2},则∁AB等于( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (0,+∞) | D. | [0,+∞) |
13.向量$\overrightarrow b=(\frac{1}{2},\frac{{\sqrt{3}}}{2})$,$\overrightarrow a•\overrightarrow b=\frac{1}{2}$,则向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |