题目内容
8.已知a=2${\;}^{\frac{1}{3}}$,b=log3$\frac{1}{2}$,c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,则( )| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
分析 利用对数函数、指数函数的单调性求解.
解答 解:∵1=20<a=2${\;}^{\frac{1}{3}}$<${2}^{\frac{1}{2}}$<1.5,
b=log3$\frac{1}{2}$<log31=0,
c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$>log${\;}_{\frac{1}{2}}$$\frac{1}{2\sqrt{2}}$=1.5,
∴c>a>b.
故选:C.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意对数函数、指数函数的单调性的合理运用.

练习册系列答案
相关题目
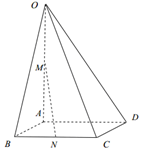 如图,在四棱锥O-ABCD中,底面ABCD是四边长为$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M为OA的中点,N为BC的中点.
如图,在四棱锥O-ABCD中,底面ABCD是四边长为$\sqrt{2}$的菱形,$∠ABC=\frac{π}{4},OA⊥$底面ABCD,OA=2,M为OA的中点,N为BC的中点. 已知函数f(x)=-x2+2x+3,x∈[-1,2)
已知函数f(x)=-x2+2x+3,x∈[-1,2) 如图,四棱锥C-ABB1A1内接于圆柱OO1,且A1A,B1B都垂直于底面圆O,BC过底面圆心O,M,N分别是棱AA1,CB1的中点,MN⊥平面CBB1.
如图,四棱锥C-ABB1A1内接于圆柱OO1,且A1A,B1B都垂直于底面圆O,BC过底面圆心O,M,N分别是棱AA1,CB1的中点,MN⊥平面CBB1.