题目内容
下列不等式中,正确的是( )
A、tan
| ||||
B、sin
| ||||
| C、sin(π-1)<sin1° | ||||
D、cos
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:利用正弦函数、余弦函数及正确函数的单调性及诱导公式对A、B、C、D四个选项逐一分析判断即可.
解答:
解:A:∵0<
<
<
,
∴tan
>0,tan
<0,故A错误;
B:∵cos(-
)=cos
=sin
>sin
,故B错误;
C:sin(π-1)=sin1≈sin57°18′>sin1°,故C错误;
D:∵
∈(π,
),∴cos
<0,而cos(-
)=cos
>0,故D正确;
故选:D.
| 2π |
| 5 |
| π |
| 2 |
| 3π |
| 4 |
∴tan
| 2π |
| 5 |
| 3π |
| 4 |
B:∵cos(-
| π |
| 7 |
| π |
| 7 |
| 5π |
| 14 |
| π |
| 5 |
C:sin(π-1)=sin1≈sin57°18′>sin1°,故C错误;
D:∵
| 7π |
| 5 |
| 3π |
| 2 |
| 7π |
| 5 |
| 2π |
| 5 |
| 2π |
| 5 |
故选:D.
点评:本题考查运用诱导公式化简求值,考查三角函数的单调性,属于中档题.

练习册系列答案
相关题目
若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,则实数k的取值范围是( )
| A、(-∞,3] |
| B、[9,+∞) |
| C、(0,9] |
| D、(-∞,9] |
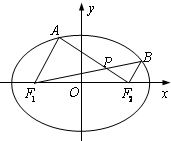 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆| x2 |
| 2 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
执行如图所示的程序框图,如果输入的t∈[-3,3],则输出的S属于( )

| A、[-6,2] |
| B、[-3,16] |
| C、[-4,5] |
| D、[-6,0] |
若f(x)=
,则f(x)的定义域为( )
| 1 | ||||
|
A、(-
| ||
| B、(-1,0) | ||
C、(-
| ||
| D、(0,+∞) |
已知sin2α=
,则sin2(α+
)=( )
| 2 |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
等比数列{an}前n项和为Sn,q=3,则
=( )
| S4 |
| a4 |
A、
| ||
B、
| ||
C、
| ||
D、
|