题目内容
A、B是单位圆O上的点,点A是单位圆与x轴正半轴的交点,点B在第二象限.记∠AOB=θ且sinθ=
.
(1)求B点坐标;
(2)求
的值.
| 4 |
| 5 |
(1)求B点坐标;
(2)求
sin(π+θ)+2sin(
| ||
| 2cos(π-θ) |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)根据角θ的终边与单位交点为(cosθ,sinθ),结合同角三角函数关系和sinθ=
,可得B点坐标;
(2)由(1)中结论,结合诱导公式化简
,代入可得答案.
| 4 |
| 5 |
(2)由(1)中结论,结合诱导公式化简
sin(π+θ)+2sin(
| ||
| 2cos(π-θ) |
解答:
解:(1)∵点A是单位圆与x轴正半轴的交点,点B在第二象限.
设B点坐标为(x,y),
则y=sinθ=
.
x=-
=-
,
即B点坐标为:(-
,
)
(2)∵
=
=
=-
.
设B点坐标为(x,y),
则y=sinθ=
| 4 |
| 5 |
x=-
| 1-sin2θ |
| 3 |
| 5 |
即B点坐标为:(-
| 3 |
| 5 |
| 4 |
| 5 |
(2)∵
sin(π+θ)+2sin(
| ||
| 2cos(π-θ) |
| -sinθ+2cosθ |
| -2cosθ |
-
| ||||
|
| 5 |
| 3 |
点评:本题考查的知识点是同角三角函数基本关系的运用,诱导公式,难度不大,属于基础题.

练习册系列答案
相关题目
下列不等式中,正确的是( )
A、tan
| ||||
B、sin
| ||||
| C、sin(π-1)<sin1° | ||||
D、cos
|
下列结论中,错误的是( )
A、x,y均为正数,则
| ||||
B、a为正数,则(1+a)(a+
| ||||
| C、lgx+logx10≥2,其中x>1 | ||||
D、
|
已知q是等比数列{an}的公比,则“q<1”是“数列{an}是递减数列”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
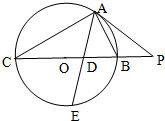 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.