题目内容
16.下列结论中:①若(x,y)在映射f的作用下的象是(x+2y,2x-y),则在映射f下,(3,1)的原象为(1,1);
②若函数f(x)满足f(x-1)=f(x+1),则f(x)的图象关于直线x=1对称;
③函数y=|3-x2|-a(a∈R)的零点个数为m,则m的值不可能为1;
④函数f(x)=log2(3x2-ax+5)在(-1,+∞)上是增函数,则实数a的取值范围是[-8,-6].
其中正确结论的序号是①③④(请将所有正确结论的序号都填上)
分析 对4个命题分别进行判断,即可得出结论.
解答 解:①设(3,1)的原象(a,b),∵(x,y)在映射f的作用下的象是(x+2y,2x-y),∴a+2b=3,2a-b=1,∴a=1,b=1,故(3,1)的原象为(1,1),正确;
②若函数f(x)满足f(x-1)=f(x+1),则f(x)的周期为2,不正确;
③函数y=|3-x2|-a(a∈R)的零点个数为0,2,3,4,则m的值不可能为1,正确;
④设g(x)=3x2-ax+5,g(x)在(-1,+∞)上是增函数,g(-1)≥0,∴$\left\{\begin{array}{l}{\frac{a}{6}≤-1}\\{8+a≥0}\end{array}\right.$,∴实数a的取值范围是[-8,-6],正确.
故答案为:①③④.
点评 本题考查映射,函数的周期性,函数的零点,复合函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
6.曲线y=$\frac{ax}{x-2}$在点(1,-a)处的切线经过点P(2,-3),则a等于( )
| A. | 1 | B. | -2 | C. | 2 | D. | -1 |
1.已知空间非零向量$\overrightarrow{{s}_{1}}$,$\overrightarrow{{s}_{2}}$,则“cos<$\overrightarrow{{s}_{1}}$,$\overrightarrow{{s}_{2}}$>=$\frac{1}{2}$”是“$\overrightarrow{{s}_{1}}$与$\overrightarrow{{s}_{2}}$的夹角为$\frac{π}{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.某几何体的三视图如图所示,则此几何体的体积等于( )
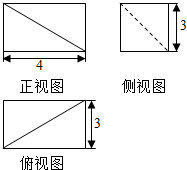

| A. | 45 | B. | 36 | C. | 30 | D. | 6 |