题目内容
11.已知p:直线y=(2m-3)x-m的图经过第一象限,q:方程$\frac{{x}^{2}}{1-m}$-y2=1表示双曲线,若命题p∧q为假,p∨q为真,求实数m的取值范围.分析 画图得到直线y=(2m-3)x-m的图经过第一象限时m的范围,再求出方程$\frac{{x}^{2}}{1-m}$-y2=1表示双曲线的m的范围,然后结合复合命题的真假判断求得实数m的取值范围.
解答 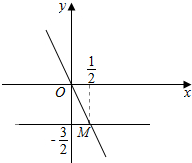 解:由y=(2m-3)x-m,得(2x-1)m-3x-y=0,
解:由y=(2m-3)x-m,得(2x-1)m-3x-y=0,
得$\left\{\begin{array}{l}{2x-1=0}\\{-3x-y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{3}{2}}\end{array}\right.$,
∴直线y=(2m-3)x-m过定点M($\frac{1}{2},-\frac{3}{2}$),
如图,若使直线y=(2m-3)x-m的图经过第一象限,则
2m-3<-3或2m-3>0,
解得:m<0或m$>\frac{3}{2}$;
若方程$\frac{{x}^{2}}{1-m}$-y2=1表示双曲线,则1-m>0,即m<1.
若命题p∧q为假,p∨q为真,
则p与q一真一假.
当p真q假时,有m$>\frac{3}{2}$;
当p假q真时,有0≤m<1.
综上,取并集可得实数m的取值范围是[0,1)∪($\frac{3}{2},+∞$).
点评 本题考查复合命题的真假判断,考查了直线系方程的应用,考查曲线为双曲线的条件,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
19.已知P:0<x<2,Q:x(x-3)<0,¬P是¬Q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.已知数列{an}是等差数列,其a1=-8,a3=-4,Sn是数列{an}的前n项和,则( )
| A. | S8<S3 | B. | S8=S3 | C. | S6<S3 | D. | S6=S3 |