��Ŀ����
1����֪�ռ��������$\overrightarrow{{s}_{1}}$��$\overrightarrow{{s}_{2}}$����cos��$\overrightarrow{{s}_{1}}$��$\overrightarrow{{s}_{2}}$��=$\frac{1}{2}$���ǡ�$\overrightarrow{{s}_{1}}$��$\overrightarrow{{s}_{2}}$�ļн�Ϊ$\frac{��}{3}$���ģ�������| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
���� �����������Ǻ����ĵ������Լ���Ҫ�������ж��ɵã�
��� �⣺�������ļн���[0����]�����Һ�����[0����]�����ݼ���
���cos$\frac{��}{3}$=$\frac{1}{2}$�ɵá�cos��$\overrightarrow{{s}_{1}}$��$\overrightarrow{{s}_{2}}$��=$\frac{1}{2}$���ǡ�$\overrightarrow{{s}_{1}}$��$\overrightarrow{{s}_{2}}$�ļн�Ϊ$\frac{��}{3}$���ij�Ҫ������
��ѡ��C��
���� ���⿼���Ҫ�������ж����漰���������Ǻ�����֪ʶ���������⣮

��ϰ��ϵ�д�
�����Ŀ
6����Բx2+y2=4��һ�㣨$\sqrt{2}$��1�������߷���Ϊ��������
| A�� | x+$\sqrt{2}$y=4 | B�� | $\sqrt{2}$x+y=3 | C�� | $\sqrt{2}$x+y=4 | D�� | x+$\sqrt{2}$y=2 |
14����֪˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$����һ�������Ľ�����Ϊm����Բ${x^2}+{y^2}-2\sqrt{5}x-2\sqrt{5}y+6=0$��������������ͬ�ĵ㵽m�ľ���Ϊ1�����˫���ߵ�������e��ȡֵ��ΧΪ��������
| A�� | $[{\frac{{\sqrt{5}}}{2}��2\sqrt{5}}]$ | B�� | $��{1��\sqrt{5}}]$ | C�� | $[{\frac{{\sqrt{5}}}{2}��\sqrt{5}}]$ | D�� | $[{\sqrt{5}��2\sqrt{5}}]$ |
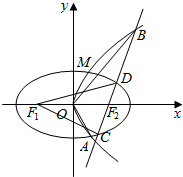 ��ͼ����ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������C2��y2=2px��p��0����������M��$\frac{2}{3}$��$\frac{2\sqrt{6}}{3}$��������ԲC1���ҽ����������C2�Ľ���F2��ͬ��
��ͼ����ԲC1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������C2��y2=2px��p��0����������M��$\frac{2}{3}$��$\frac{2\sqrt{6}}{3}$��������ԲC1���ҽ����������C2�Ľ���F2��ͬ��