题目内容
由某种设备的使用年限xi(年)与所支出的维修费yi(万元)的数据资料算得如下结果,
xi2=90,
xiyi=112,
xi=20,
yi=25.
(1)求所支出的维修费y对使用年限x的线性回归方程
=
x+
;
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
(附:在线性回归方程
=
x+
中,
=
,
=
-
,其中
,
为样本平均值.)
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
(1)求所支出的维修费y对使用年限x的线性回归方程
 |
| y |
 |
| b |
 |
| a |
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
(附:在线性回归方程
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
. |
| x |
. |
| y |
考点:线性回归方程
专题:概率与统计
分析:(1)利用已知条件求出样本中心坐标,以及
=
,代入回归直线方程,求出
,即可求所支出的维修费y对使用年限x的线性回归方程
=
x+
;
(2)①直接利用回归直线方程的斜率,判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,代入回归直线方程,即可估计支出的维修费的值.
 |
| b |
| |||||||
|
 |
| a |
 |
| y |
 |
| b |
 |
| a |
(2)①直接利用回归直线方程的斜率,判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,代入回归直线方程,即可估计支出的维修费的值.
解答:
解:(1)∵
xi=20,
yi=25,∴
=
xi=4,
=
yi=5
∴
=
=
=1.2…(3分)
=
-
=5-1.2×4=0.2…(5分)
∴线性回归方程
=1.2x+0.2. …(6分)
(2)①由(1)知
=1.2>0,∴变量x与y之间是正相关. …(9分)
②由(1)知,当x=8时,
=9.8(万元),即使用年限为8年时,支出的维修费约是9.8万元.
…(12分)
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
. |
| x |
| 1 |
| 5 |
| 5 |
 |
| i=1 |
. |
| y |
| 1 |
| 5 |
| 5 |
 |
| i=1 |
∴
| ? |
| b |
| |||||||
|
| 112-5×4×5 |
| 90-5×42 |
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
∴线性回归方程
| ? |
| y |
(2)①由(1)知
| ? |
| b |
②由(1)知,当x=8时,
| ? |
| y |
…(12分)
点评:本题考查线性回归方程的求法,本题解题的关键是根据所给的条件求出直线的样本中心点,线性回归方程一定过样本中心点是本题解题的依据,本题是一个基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知函数f(x)=
若直线y=m与函数f(x)的图象有两个不同的交点,则实数m的取值范围是( )
|
| A、m∈R | B、m>1 |
| C、m>0 | D、0<m<1 |
已知函数f(x)=ex-2x+a有零点,则实数a的取值范围是( )
| A、(-∞,2ln2-2] |
| B、[2ln2-2,+∞) |
| C、[2ln2,+∞) |
| D、[2ln2-2,2ln2] |
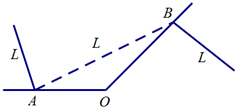 如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.
如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.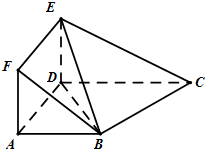 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,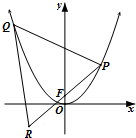 已知抛物线C:y=ax2,直线y=x+
已知抛物线C:y=ax2,直线y=x+