Question

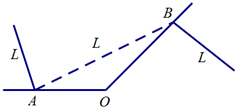如图，某城市有一条公路从正西方AO通过市中心O后转向东北方OB，现要修筑一条铁路L，L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，为了市民出行方便与城市环境问题，现要求市中心O到AB的距离为10km，设∠OAB=α．
（1）试求AB关于角α的函数关系式；
（2）问把A、B分别设在公路上离市中心O多远处，才能使AB最短，并求其最短距离．

Answer 1

考点：正弦定理,余弦定理

专题：应用题

分析：（1）作OM垂直AB，垂足为M，则OM=10，由题意∠AOB=135°，在△AOB中，利用正弦定理表示出AB，在△MOB中，表示出OB，最后利用正弦定理求得AB．
（2）先表示出AB，根据α的范围确定AB的最小值，及此时α的值，进而求得OA．

解答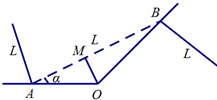： 解（1）如图，作OM垂直AB，垂足为M，则OM=10，
由题意∠AOB=135°，α∈（0°，45°），∠OBA=45°-α．  
在△AOB中，由正弦定理得

AB

sin135°

=

OB

sinα

，即AB=

2

2

•

OB

sinα

．
在△MOB中，OB=

10

sin(45°-α)

，
∴AB=

2

2

•

OB

sinα

=

2

2

•

10

sinαsin(45°-α)

=5

2

1

sinαsin(45°-α)

．
（2）AB=

2

2

•

10

sinα(sin45°cosα-cos45°sinα)

=

10

sinαcosα-sin2α

=

20

sin2α+cos2α-1

=

20

2 sin(2α+45°)-1

．
因为α∈（0°，45°），所以当α=22.5°时有AB的最小值20(

2

+1)．
此时，OA=OB=

10

sin22.5°

=10

4+2 2

．
答：A，B都设在公路上离市中心10

4+2 2

km处，才能使AB最短，其最短距离是20(

2

+1)km．

点评：本题主要考查了正弦定理的实际应用．考查了学生运用所学知识解决实际问题的能力．