题目内容
曲线ρ=2
sinθ-2cosθ上离极点最远的点的极坐标为 .
| 3 |
考点:简单曲线的极坐标方程
专题:选作题,坐标系和参数方程
分析:曲线ρ=2
sinθ-2cosθ可化为直角坐标,求出离原最远的点的直角坐标,可得离极点最远的点的极坐标.
| 3 |
解答:
解:曲线ρ=2
sinθ-2cosθ可化为曲线ρ2=2
ρsinθ-2ρcosθ,即x2+y2=2
y-2x,
即:(x+1)2+(y-
)2=4,圆心为C(-1,
),半径为2,
∴OC方程为y=-
x,
代入圆的方程可得x=0或-2,
x=-2时,y=2
,极坐标为(4,
).
故答案为:(4,
).
| 3 |
| 3 |
| 3 |
即:(x+1)2+(y-
| 3 |
| 3 |
∴OC方程为y=-
| 3 |
代入圆的方程可得x=0或-2,
x=-2时,y=2
| 3 |
| 2π |
| 3 |
故答案为:(4,
| 2π |
| 3 |
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
相关题目


 某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.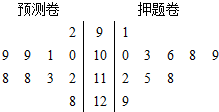 四川一所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟模拟考试,检测成绩的茎叶图如图所示.
四川一所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟模拟考试,检测成绩的茎叶图如图所示.
 如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为
如图是某个四面体的三视图,若在该四面体的外接球内任取一点,则点落在四面体内的概率为