Question

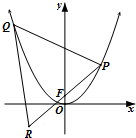已知抛物线C：y=ax²，直线y=x+

1

4

经过抛物线的焦点F．
（Ⅰ）求抛物线C的方程；
（Ⅱ）设P（x₀，y₀）（x₀≠0）是抛物线上一点，过点P且与P处的切线垂直的直线l与抛物线C的另一个交点为Q，P点关于焦点F的对称点为R，求△PQR面积的最小值和此时P点的坐标．

Answer 1

考点：直线与圆锥曲线的综合问题,抛物线的标准方程,直线与圆锥曲线的关系

专题：圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题

分析：（Ⅰ）求出抛物线的焦点坐标，即可求抛物线C的方程；
（Ⅱ）设P（x₀，y₀）（x₀≠0）是抛物线上一点，推出直线PQ的方程，与抛物线联立，利用弦长公式，点到直线的距离，表示出三角形的面积，通过函数的导数，求解△PQR面积的最小值和此时P点的坐标．

解答： 解：（Ⅰ）焦点F(0，

1

4a

)，∴

1

4a

=

1

4

即a=1∴抛物线C：x²=y-------------------------（3分）
（Ⅱ）设P(x0，x02)，Q(x1，x12)，F(0，

1

4

)，∴R(-x0，

1

2

-x02)---------------------------（4分）
lPQ：y-x02=-

1

2x0

(x-x0)即y=-

1

2x 0

x+

1

2

+x02
联立

y=- 1 2x0 x+ 1 2 +x02 x2=y

，得x2+

1

2x0

x-(

1

2

+x02)=0
得

x 0+x1=- 1 2x0 x0+x1=-( 1 2 +x02)

--------------------------------------------------------------（7分）
∴|PQ|=

1+ 1 4x02

|x0-x1|=

(1+ 1 4x02 )( 1 4x02 +4x02+2)

----------------------（9分）
点R(-x0，

1

2

-x02)到PQ的距离d=

|2x02+ 1 2 |

1+ 1 4x02

------------------------------------（11分）
∴S△PQR=

1

2

|PQ|•d=

1

2

|2x02+

1

2

|

1 4x02 +4x02+2

=

1

8

(4x02+1)2

|x0|

记f(x)=

(4x2+1)2

x

(x＞0)
则f(x)=16x3+8x+

1

x

，f/(x)=48x2+8-

1

x2

=

(4x2+1)(12x2-1)

x2

当x2=

1

12

时f（x）取得最小值．
故△PQR的面积的最小值为

4 3

9

，此时P(±

3

6

，

1

12

)--------------------------------（14分）

点评：本题主要考查抛物线几何性质，直线与抛物线的位置关系，同时考查解析几何的基本思想方法和运算能力．