题目内容
先后抛掷一枚骰子,记向上的点数为a,b.事件A:点(a,b)落在圆x2+y2=12内;事件B:f(a)<0,其中函数f(x)=x2-(2t+1)x+t(t+1),t为常数.已知P(B)>0
(1)求P(A);
(2)当t=
时,求P(B);
(3)如A、B同时发生的概率P(AB)=
,求t的取值范围.
(1)求P(A);
(2)当t=
| 1 |
| 2 |
(3)如A、B同时发生的概率P(AB)=
| 1 |
| 36 |
考点:古典概型及其概率计算公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)先计算出先后抛掷一枚骰子两次的基本事件总数,及满足a2+b2<12的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)将t=
代入,计算满足f(a)<0的基本事件个数,代入古典概型概率计算公式,可得答案.
(3)分类讨论满足P(AB)=
的t的取值范围,最后综合讨论结果,可得答案.
(2)将t=
| 1 |
| 2 |
(3)分类讨论满足P(AB)=
| 1 |
| 36 |
解答:
解:(1)先后抛掷一枚骰子两次共有36种不同情况,
其中满足落在圆x2+y2=12内的点(a,b),即a2+b2<12有:
(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)共6个,
故P(A)=
=
,
(2)当t=
时,f(x)=x2-2x+
,
解f(x)=x2-2x+
<0得x∈(
,
),则a只能取1
∴P(B)=
,
(3)∵f(x)=x2-(2t+1)x+t(t+1)<0解集为(t,t+1),满
足f(a)<0的a只可能在1、2、3、4、5、6中取一个,
∴当a=1时,AB={(1,1),(1,2),(1,3)};
如a=2,AB={(2,1),(2,2)};
如a=3,AB={(3,1)}
如a取4、5、6,AB=∅
则只有a=3满足P(AB)=
,
则t∈(2,3)
其中满足落在圆x2+y2=12内的点(a,b),即a2+b2<12有:
(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)共6个,
故P(A)=
| 6 |
| 36 |
| 1 |
| 6 |
(2)当t=
| 1 |
| 2 |
| 3 |
| 4 |
解f(x)=x2-2x+
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
∴P(B)=
| 1 |
| 6 |
(3)∵f(x)=x2-(2t+1)x+t(t+1)<0解集为(t,t+1),满
足f(a)<0的a只可能在1、2、3、4、5、6中取一个,
∴当a=1时,AB={(1,1),(1,2),(1,3)};
如a=2,AB={(2,1),(2,2)};
如a=3,AB={(3,1)}
如a取4、5、6,AB=∅
则只有a=3满足P(AB)=
| 1 |
| 36 |
则t∈(2,3)
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知i为虚数单位,则复数
等于( )
| (2+i)(1-i)2 |
| 1-2i |
| A、2 | B、-2 | C、2i | D、-2i |
已知F1,F2为双曲线
-
=1(a>0,b>0)的左右焦点,M为此双曲线上的一点,满足|MF1|=3|MF2|,那么此双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) |
| B、(1,2] |
| C、(0,2) |
| D、[2,+∞) |
如图所示的流程图,若输入x的值为2,则输出x的值为( )


| A、5 | B、7 | C、125 | D、127 |
若点P在三个顶点坐标分别为C(0,0),A(0,2
),B(2,0)的△ABC内运动,则动点P到顶点A的距离|PA|<2
的概率为( )
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|


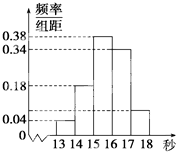 为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.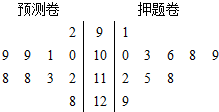 四川一所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟模拟考试,检测成绩的茎叶图如图所示.
四川一所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟模拟考试,检测成绩的茎叶图如图所示.