题目内容
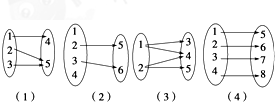
如图给出的四个对应关系，其中构成映射的是（ ）
| A、（1）（2） |
| B、（1）（4） |
| C、（1）（2）（4） |
| D、（3）（4） |
考点：映射
专题：计算题,函数的性质及应用
分析：根据映射的定义，在集合A中的任意一个元素，在集合B中都有唯一确定的元素与之对应．
解答：
解：（1）（4）可以构成映射；
在（2）中，1，4在后一个集合中找不到对应的元素，故不是映射；
在（3）中，1对应了两个数3，4，故也不是映射；
故选B．
在（2）中，1，4在后一个集合中找不到对应的元素，故不是映射；
在（3）中，1对应了两个数3，4，故也不是映射；
故选B．
点评：本题考查了映射的定义，属于基础题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知集合A={1，2，3，4}，B={5，6}，设映射f：A→B使集合B中的元素在A中都有原象，这样的映射个数共有（ ）
| A、16 | B、14 | C、15 | D、12 |
已知a，b∈R，函数f（x）=tanx在x=-
处与直线y=ax+b+
相切，设g（x）=-bxlnx+a在定义域内（ ）
| π |
| 4 |
| π |
| 2 |
A、有极大值
| ||
B、有极小值
| ||
C、有极大值2-
| ||
D、有极小值2-
|