题目内容
已知集合A={1，2，3，4}，B={5，6}，设映射f：A→B使集合B中的元素在A中都有原象，这样的映射个数共有（ ）
| A、16 | B、14 | C、15 | D、12 |
考点：映射
专题：函数的性质及应用
分析：先求出映射f：A→B的个数和集合B中的元素不都是A中元素在f下的象的映射的个数，从而得到集合B中的元素都是A中元素在f下的象的映射的个数．
解答：
解：∵集合A中的元素1，2，3，4各有2种对应情况，
∴映射f：A→B的个数是2×2×2×2=16个．
∵集合B中的元素不都是A中元素在f下的象的映射有2个，
∴集合B中的元素都是A中元素在f下的象的映射一共有16-2=14个．
故选：B
∴映射f：A→B的个数是2×2×2×2=16个．
∵集合B中的元素不都是A中元素在f下的象的映射有2个，
∴集合B中的元素都是A中元素在f下的象的映射一共有16-2=14个．
故选：B
点评：本题考查映射的概念和应用，解题时要认真审题，仔细求解．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
在△ABC中，A=60°，a=3，则
=（ ）
| a+b+c |
| sinA+sinB+sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
如图给出的四个对应关系，其中构成映射的是（ ）
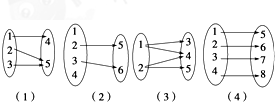
| A、（1）（2） |
| B、（1）（4） |
| C、（1）（2）（4） |
| D、（3）（4） |
下列命题中，真命题是（ ）
| A、命题“若p，则q．”的否命题是“若p，则￢q．” | ||
| B、命题p：?x∈R，使得x2+1＜0，则?p：?x∈R，使得x2+1≥0 | ||
| C、已知命题p、q，若“p∨q”为假命题，则命题p与q一真一假 | ||
D、a+b=0的充要条件是
|
已知x
-（log
0.5）x＜（-y）
-（log
0.5）-y，则实数x，y的关系是（ ）
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、x-y＞0 |
| B、x-y＜0 |
| C、x+y＞0 |
| D、x+y＜0 |