题目内容
已知函数f(x)=x+
.
(1)若命题p:“存在x∈[
,4],使f(log2x)-k•log2x≥2”是真命题,求实数k的取值范围;
(2)设g(x)=|2x-1|,方程f[g(x)]+
=3k+2有三个不同的实数解,求实数k的取值范围.
| 1 |
| x |
(1)若命题p:“存在x∈[
| 2 |
(2)设g(x)=|2x-1|,方程f[g(x)]+
| 2k |
| g(x) |
考点:函数恒成立问题,特称命题
专题:函数的性质及应用,不等式的解法及应用
分析:(1)把命题存在x∈[
,4],使f(log2x)-k•log2x≥2”是真命题转化为不等式恒成立,换元后分分离参数k,利用配方法求出二次函数最值得答案;
(2)把已知方程转化为|2x-1|2-(3k+2)•|2x-1|+(2k+1)=0,令|2x-1|=t,则原方程有三个不同的实数解转化为t2-(3k+2)t+(2k+1)=0有两个不同的实数解t1,t2,其中0<t1<1,t2>1或0<t1<1,t2=1.然后运用“三个二次”的结合列式得答案.
| 2 |
(2)把已知方程转化为|2x-1|2-(3k+2)•|2x-1|+(2k+1)=0,令|2x-1|=t,则原方程有三个不同的实数解转化为t2-(3k+2)t+(2k+1)=0有两个不同的实数解t1,t2,其中0<t1<1,t2>1或0<t1<1,t2=1.然后运用“三个二次”的结合列式得答案.
解答:
解:(1)f(log2x)-k•log2x≥2可化为log2x+
-2≥k•log2x,
设
=t,
∵x∈[
,4],∴t∈[
,2].
∴不等式可化为k≤t2-2t+1.
记h(t)=t2-2t+1,∵t∈[
,2],故h(t)max=1.
∴k的取值范围是(-∞,1];
(2)方程f[g(x)]+
=3k+2化为|2x-1|2-(3k+2)•|2x-1|+(2k+1)=0.
令|2x-1|=t,则t∈(0,+∞),t2-(3k+2)t+(2k+1)=0有两个不同的实数解t1,t2,
其中0<t1<1,t2>1或0<t1<1,t2=1.
记h(t)=t2-(3k+2)t+(2k+1),则
①或
②
解①得,k>0;②无解.
∴实数k的取值范围为(0,+∞).
| 1 |
| log2x |
设
| 1 |
| log2x |
∵x∈[
| 2 |
| 1 |
| 2 |
∴不等式可化为k≤t2-2t+1.
记h(t)=t2-2t+1,∵t∈[
| 1 |
| 2 |
∴k的取值范围是(-∞,1];
(2)方程f[g(x)]+
| 2k |
| g(x) |
令|2x-1|=t,则t∈(0,+∞),t2-(3k+2)t+(2k+1)=0有两个不同的实数解t1,t2,
其中0<t1<1,t2>1或0<t1<1,t2=1.
记h(t)=t2-(3k+2)t+(2k+1),则
|
|
解①得,k>0;②无解.
∴实数k的取值范围为(0,+∞).
点评:本题考查了函数恒成立问题,考查了数学转化思想方法,关键是对题意得理解,考查了学生的逻辑思维能力,是压轴题.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
在△ABC中,A=60°,a=3,则
=( )
| a+b+c |
| sinA+sinB+sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
如图给出的四个对应关系,其中构成映射的是( )
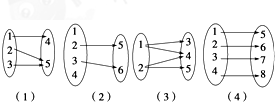

| A、(1)(2) |
| B、(1)(4) |
| C、(1)(2)(4) |
| D、(3)(4) |
等差数列{an}共有3m项,若前2m项的和为200,前3m项的和为225,则中间m项的和为( )
| A、50 | B、75 |
| C、100 | D、125 |
