题目内容
设集合A为函数f(x)=ln(-x2-2x+8)的定义域,集合B为不等式(ax-
)(x+4)≤0的解集.
(Ⅰ) 写出f(x)的单调区间;
(Ⅱ) 若B⊆∁RA,求a的取值范围.
| 1 |
| a |
(Ⅰ) 写出f(x)的单调区间;
(Ⅱ) 若B⊆∁RA,求a的取值范围.
考点:集合的包含关系判断及应用
专题:函数的性质及应用,集合
分析:(Ⅰ)先求出集合A=(-4,2),二次函数-x2-2x+8在(-4,-1)单调递减,在[-1,2)单调递增,根据复合函数的单调性即可写出f(x)的单调区间;
(Ⅱ)求出∁RA,讨论a>0,a<0写出集合B,根据B⊆∁RA,即可写出限制a的不等式,解不等式即得a的取值范围.
(Ⅱ)求出∁RA,讨论a>0,a<0写出集合B,根据B⊆∁RA,即可写出限制a的不等式,解不等式即得a的取值范围.
解答:
解:(Ⅰ)由-x2-2x+8>0,解得A=(-4,2);
根据复合函数的单调性知,f(x)的单调递增区间为(-4,-1),单调递减区间[-1,2);
(Ⅱ)因为∁RA=(-∞,-4]∪[2,+∞).
由(ax-
)(x+4)≤0,得a(x-
)(x+4)≤0;
若a>0,B=[-4,
],不满足B⊆∁RA;
若a<0,B=(-∞,-4]∪[
,+∞),要使B⊆∁RA,则:
≥2,解得-
≤a<0,或0<a≤
;
又a<0,∴-
≤a<0;
综上得a的取值范围是[-
,0).
根据复合函数的单调性知,f(x)的单调递增区间为(-4,-1),单调递减区间[-1,2);
(Ⅱ)因为∁RA=(-∞,-4]∪[2,+∞).
由(ax-
| 1 |
| a |
| 1 |
| a2 |
若a>0,B=[-4,
| 1 |
| a2 |
若a<0,B=(-∞,-4]∪[
| 1 |
| a2 |
| 1 |
| a2 |
| ||
| 2 |
| ||
| 2 |
又a<0,∴-
| ||
| 2 |
综上得a的取值范围是[-
| ||
| 2 |
点评:考查复合函数的单调性及取得单调区间的情况,子集、补集的概念.

练习册系列答案
相关题目
如图给出的四个对应关系,其中构成映射的是( )
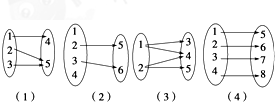

| A、(1)(2) |
| B、(1)(4) |
| C、(1)(2)(4) |
| D、(3)(4) |
下列命题中,真命题是( )
| A、命题“若p,则q.”的否命题是“若p,则¬q.” | ||
| B、命题p:?x∈R,使得x2+1<0,则?p:?x∈R,使得x2+1≥0 | ||
| C、已知命题p、q,若“p∨q”为假命题,则命题p与q一真一假 | ||
D、a+b=0的充要条件是
|
等差数列{an}共有3m项,若前2m项的和为200,前3m项的和为225,则中间m项的和为( )
| A、50 | B、75 |
| C、100 | D、125 |
| m |
| n |
| m |
| n |
| A、0 | ||
B、
| ||
C、
| ||
| D、8 |