题目内容
已知一个直角三角形的两条直角边长为a,b,求该直角三角形内切圆的面积,试设计求解该问题的算法,并画出程序框图.
考点:设计程序框图解决实际问题
专题:算法和程序框图
分析:首先根据勾股定理求得该直角三角形的斜边是
,再根据其内切圆的半径等于两条直角边的和与斜边的差的一半,有r=
,内切圆的面积S=πr2进行计算即可.
| a2+b2 |
a+b-
| ||
| 2 |
解答:
解:算法如下:
第一步,输入两条直角边长为a,b.
第二步,计算r=
.
第三步,计算S=πr2.
第四步,输出S.
程序框图如下:

第一步,输入两条直角边长为a,b.
第二步,计算r=
a+b-
| ||
| 2 |
第三步,计算S=πr2.
第四步,输出S.
程序框图如下:

点评:此题要熟记直角三角形内切圆的半径公式:内切圆的半径等于两条直角边的和与斜边的差的一半,主要考察设计程序框图解决实际问题,属于基础题.

练习册系列答案
相关题目
如图给出的四个对应关系,其中构成映射的是( )
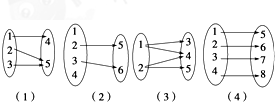

| A、(1)(2) |
| B、(1)(4) |
| C、(1)(2)(4) |
| D、(3)(4) |