题目内容
作出函数f(x)=2|x|的图象,并根据图象判断f(
)与
的大小.
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
考点:指数函数单调性的应用
专题:函数的性质及应用
分析:作出函数图象,f(
)和
的在函数图象中的意义可判断f(
)<
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
解答:
解:作出函数图象如下图:
f
f(
)意义为D点的纵坐标,
的意义为AB中点的纵坐标,据图可判断f(
)<
f

f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
点评:本题考查了数形结合的方法比较大小,理解代数式的几何意义是重点.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
如图给出的四个对应关系,其中构成映射的是( )
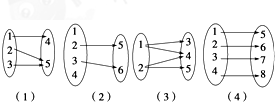

| A、(1)(2) |
| B、(1)(4) |
| C、(1)(2)(4) |
| D、(3)(4) |
已知x,y满足
,则z=x-2y的最大值是( )
|
| A、-5 | B、-2 | C、-1 | D、1 |