题目内容
已知点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,给出下列说法:
①3a-4b+10>0;
②
>2;
③当a>0时,a+b有最小值,无最大值;
④当a>0且a≠1,b>0时,
的取值范围为(-∞,-
)∪(
,+∞).
其中正确的个数是( )
①3a-4b+10>0;
②
| a2+b2 |
③当a>0时,a+b有最小值,无最大值;
④当a>0且a≠1,b>0时,
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
其中正确的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用,直线的斜率
专题:简易逻辑
分析:画出图象,利用点与直线的位置关系判断①的正误;两点之间的距离判断②的正误;利用图象判断③的正误;利用直线的斜率判断④的正误;
解答:
 解:点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,
解:点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,
3×1-4×0+10>0,3a-4b+10<0,所以①不正确;
原点到直线的距离为:
=2,
∴
>2;所以②正确.
对于③,可知,A的可行域,不含边界,所以③不正确.
对于④,当a>0且a≠1,b>0时,
表示可行域内的点与(1,0)连线的斜率,它的取值范围为(-∞,-
)∪(
,+∞).正确,
正确的命题两个.
故选:B.
 解:点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,
解:点A(a,b)与点B(1,0)在直线3x-4y+10=0的两侧,3×1-4×0+10>0,3a-4b+10<0,所以①不正确;
原点到直线的距离为:
| |10| | ||
|
∴
| a2+b2 |
对于③,可知,A的可行域,不含边界,所以③不正确.
对于④,当a>0且a≠1,b>0时,
| b |
| a-1 |
| 5 |
| 2 |
| 3 |
| 4 |
正确的命题两个.
故选:B.

点评:本题考查命题的真假的判断,线性规划的应用,考查计算能力.

练习册系列答案
相关题目
如图给出的四个对应关系,其中构成映射的是( )
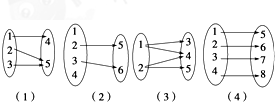

| A、(1)(2) |
| B、(1)(4) |
| C、(1)(2)(4) |
| D、(3)(4) |
等差数列{an}共有3m项,若前2m项的和为200,前3m项的和为225,则中间m项的和为( )
| A、50 | B、75 |
| C、100 | D、125 |
已知x
-(log
0.5)x<(-y)
-(log
0.5)-y,则实数x,y的关系是( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、x-y>0 |
| B、x-y<0 |
| C、x+y>0 |
| D、x+y<0 |
| m |
| n |
| m |
| n |
| A、0 | ||
B、
| ||
C、
| ||
| D、8 |