题目内容
已知a,b∈R,函数f(x)=tanx在x=-
处与直线y=ax+b+
相切,设g(x)=-bxlnx+a在定义域内( )
| π |
| 4 |
| π |
| 2 |
A、有极大值
| ||
B、有极小值
| ||
C、有极大值2-
| ||
D、有极小值2-
|
考点:正切函数的图象
专题:三角函数的图像与性质
分析:先求出f′(x)=
,再由条件根据导数的几何意义可得 a=f′(-
)=2.再把切点(-
,2)代入切线方程求得b,可得g(x)解析式.再根据g′(x)的符号,求出g(x)的单调区间,从而求得g(x)的极值.
| 1 |
| cos2x |
| π |
| 4 |
| π |
| 4 |
解答:
解:由函数f(x)=tanx,可得f′(x)=
.
再根据函数f(x)=tanx在x=-
处与直线y=ax+b+
相切,可得 a=f′(-
)=2.
再把切点(-
,2)代入直线y=ax+b+
,可得b=-1,∴g(x)=xlnx+1,g′(x)=lnx+1.
令g′(x)=lnx+1=0,求得x=
,在(0,
)上,g′(x)<0,在(
,+∞)上,g′(x)>0,
故g(x)在其定义域(0,+∞)上存在最小值为g(
)=2-
,
故选:D.
| 1 |
| cos2x |
再根据函数f(x)=tanx在x=-
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
再把切点(-
| π |
| 4 |
| π |
| 2 |
令g′(x)=lnx+1=0,求得x=
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
故g(x)在其定义域(0,+∞)上存在最小值为g(
| 1 |
| e |
| 1 |
| e |
故选:D.
点评:本题主要考查函数在某处的导数的几何意义,利用导数求函数的极值,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
在△ABC中,A=60°,a=3,则
=( )
| a+b+c |
| sinA+sinB+sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
如图给出的四个对应关系,其中构成映射的是( )
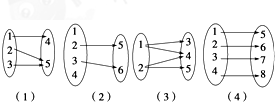

| A、(1)(2) |
| B、(1)(4) |
| C、(1)(2)(4) |
| D、(3)(4) |
下列命题中,真命题是( )
| A、命题“若p,则q.”的否命题是“若p,则¬q.” | ||
| B、命题p:?x∈R,使得x2+1<0,则?p:?x∈R,使得x2+1≥0 | ||
| C、已知命题p、q,若“p∨q”为假命题,则命题p与q一真一假 | ||
D、a+b=0的充要条件是
|
等差数列{an}共有3m项,若前2m项的和为200,前3m项的和为225,则中间m项的和为( )
| A、50 | B、75 |
| C、100 | D、125 |