题目内容
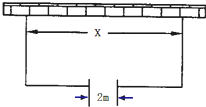如图，围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的一扇门，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，一扇门的造价为600元，设利用的旧墙的长度为xm，总造价为y元．（1）将y表示为x的函数；
（2）试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用．
考点：基本不等式,函数解析式的求解及常用方法
专题：函数的性质及应用,不等式的解法及应用
分析：（1）如图，设矩形的另一边长为am，由题意可得y=45x+180（x-2）+180•2a+600，利用矩形的面积可得xa=360，代入消去a可得y=225x+
+240（x＞0）．
（2）利用基本不等式即可得出．
| 129600 |
| x |
（2）利用基本不等式即可得出．
解答：
解：（1）如图，设矩形的另一边长为am，
则y=45x+180（x-2）+180•2a+600=225x+360a+240，
由已知xa=360，得a=
，
∴y=225x+
+240（x＞0）．
（2）∵x＞0，∴y≥2
+240=11040．
当且仅当225x=
时，即x=24等号成立．
∴当x=24m时，修建围墙的总费用最小，最小总费用是11040元．
则y=45x+180（x-2）+180•2a+600=225x+360a+240，
由已知xa=360，得a=
| 360 |
| x |
∴y=225x+
| 129600 |
| x |
（2）∵x＞0，∴y≥2
225x•
|
当且仅当225x=
| 3602 |
| x |
∴当x=24m时，修建围墙的总费用最小，最小总费用是11040元．
点评：本题考查了矩形的面积计算公式、基本不等式的性质，考查了计算能力，属于中档题．
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
在△ABC中，已知a=2
，b=
，A=130°，则此三角形（ ）
| 3 |
| 7 |
| 2 |
| A、无解 | B、只有一解 |
| C、有两解 | D、解的个数不确定 |