题目内容
若在区间[-5,5]内任取一个实数a,则使直线x+y+a=0与圆(x-1)2+(y+2)2=2有公共点的概率为 .
考点:几何概型
专题:计算题,概率与统计
分析:利用圆心到直线的距离小于等于半径可得到直线与圆有公共点,可求出满足条件的a,最后根据几何概型的概率公式可求出所求.
解答:
解:∵直线x+y+a=0与圆(x-1)2+(y+2)2=2有公共点,
∴
≤
,解得-1≤a≤3,
∴在区间[-5,5]内任取一个实数a,使直线x+y+a=0与圆(x-1)2+(y+2)2=2有公共点的概率为
=
故答案为:
.
∴
| |1-2+a| | ||
|
| 2 |
∴在区间[-5,5]内任取一个实数a,使直线x+y+a=0与圆(x-1)2+(y+2)2=2有公共点的概率为
| 3+1 |
| 5+5 |
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题主要考查了几何概型的概率,以及直线与圆相交的性质,解题的关键弄清概率类型,同时考查了计算能力,属于基础题.

练习册系列答案
相关题目
已知等比数列{an},若a1+a2=20,a3+a4=80,则a5+a6等于( )
| A、480 | B、120 |
| C、240 | D、320 |
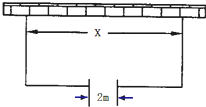 如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.
如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.