题目内容
已知函数f(x)=x2-2ax+3,当x∈(0,2]时,f(x)≥0恒成立,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:将二次函数进行配方,利用二次函数的图象和性质求解,要使不等式f(x)≥0恒成立,则只需求出函数在x∈[0,2]时的最小值即可
解答:
解:x∈(0,2]时,f(x)≥0恒成立,
即a≤
+
在(0,2]恒成立,
令g(x)=
+
,x∈(0,2],
∴g(x)=
+
≥2
=
,当且仅当x=
时,“=”成立,
∴a≤
.
即a≤
| x |
| 2 |
| 3 |
| 2x |
令g(x)=
| x |
| 2 |
| 3 |
| 2x |
∴g(x)=
| x |
| 2 |
| 3 |
| 2x |
|
| 3 |
| 3 |
∴a≤
| 3 |
点评:本题主要考查二次函数的图象和性质,要注意分别讨论对称轴和区间之间的关系确定函数的最小值.

练习册系列答案
相关题目
等差数列的相邻4项分别是a+1,a+3,b,a+b,那么a,b的值依次为( )
| A、2,7 | B、1,6 |
| C、0,5 | D、无法确定 |
已知等比数列{an},若a1+a2=20,a3+a4=80,则a5+a6等于( )
| A、480 | B、120 |
| C、240 | D、320 |
下列不等关系成立的是( )
| A、sin31°>cos59° |
| B、-cos59°>-cos61° |
| C、tan31°>tan61° |
| D、sin59°>cos59° |
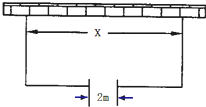 如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.
如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.