题目内容
已知△ABC中,角A,B,C的对边分别为a,b,c,且c•cosB-(2a-b)(2cos2
-1)=0.
(1)求角C的大小;
(2)若c=2
,S△ABC=2
,求边a,b的值.
| C |
| 2 |
(1)求角C的大小;
(2)若c=2
| 3 |
| 3 |
考点:正弦定理,三角函数中的恒等变换应用
专题:解三角形
分析:(1)利用正弦定理把等式中边转化成角的正弦,整理求得cosC,进而求得C.
(2)利用余弦定理和c的值,求得a和b的关系式,通过面积公式求得a和b的另一关系式,联立方程求得a和b.
(2)利用余弦定理和c的值,求得a和b的关系式,通过面积公式求得a和b的另一关系式,联立方程求得a和b.
解答:
解:(1)∵c•cosB-(2a-b)(2cos2
-1)=0.
∴sinCcosB-2sinAcosC+sinBcosC=0,
∴sin(B+C)=2sinAcosC,
∴sinA=2sinAcosC,
∴cosC=
,
∵0<C<π,
∴C=
.
(2)S=
absinC=2
,
∴ab=8,①
∵cosC=
=
=
,
∴a2+b2=20,②
由①②求得a=2,b=4或a=4
,b=
.
| C |
| 2 |
∴sinCcosB-2sinAcosC+sinBcosC=0,
∴sin(B+C)=2sinAcosC,
∴sinA=2sinAcosC,
∴cosC=
| 1 |
| 2 |
∵0<C<π,
∴C=
| π |
| 3 |
(2)S=
| 1 |
| 2 |
| 3 |
∴ab=8,①
∵cosC=
| a2+b2-c2 |
| 2ab |
| a2+b2-12 |
| 16 |
| 1 |
| 2 |
∴a2+b2=20,②
由①②求得a=2,b=4或a=4
| 2 |
| 2 |
点评:本题主要考查了正弦定理和余弦定理的综合运用.考查了学生的推理和运算能力.

练习册系列答案
相关题目
已知f(x)=ln(
-3x)+1,则f(lg3)+f(lg
)等于( )
| 1+9x2 |
| 1 |
| 3 |
| A、2 | B、1 | C、0 | D、-1 |
已知等比数列{an},若a1+a2=20,a3+a4=80,则a5+a6等于( )
| A、480 | B、120 |
| C、240 | D、320 |
 某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r-3(l为圆柱的高,r为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为c千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.
某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形,l=2r-3(l为圆柱的高,r为球的半径,l≥2).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为c千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为y千元.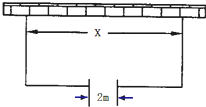 如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.
如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.