题目内容
设A={-4，2a-1，a2}，B={a-1，1-a，9}，已知A∩B={9}，求a的值．
考点：交集及其运算
专题：集合
分析：根据A与B的交集中元素为9，得到9属于A且属于B，即可确定出a的值．
解答：
解：∵A={-4，2a-1，a2}，B={a-1，1-a，9}，且A∩B={9}，
∴9∈A且9∈B，
可得2a-1=9或a2=9，解得：a=5或a=±3，
当a=5时，A={-4，9，25}，B={4，-4，9}，则有A∩B={-4，9}，不合题意，故a=5舍去；
当a=3时，A={-4，5，9}，B={2，-2，9}，此时A∩B={9}，符合题意；
当a=-3时，A={-4，-7，9}，B={-8，4，9}，此时A∩B={9}，符合题意，
则a=3或-3．
∴9∈A且9∈B，
可得2a-1=9或a2=9，解得：a=5或a=±3，
当a=5时，A={-4，9，25}，B={4，-4，9}，则有A∩B={-4，9}，不合题意，故a=5舍去；
当a=3时，A={-4，5，9}，B={2，-2，9}，此时A∩B={9}，符合题意；
当a=-3时，A={-4，-7，9}，B={-8，4，9}，此时A∩B={9}，符合题意，
则a=3或-3．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn，且满足S4+a25=5，则一定有（ ）
| A、a6是常数 |
| B、S7是常数 |
| C、a13是常数 |
| D、S13是常数 |
某加油站拟造如图所示的铁皮储油罐（不计厚度，长度单位：米），其中储油罐的中间为圆柱形，左右两端均为半球形，l=2r-3（l为圆柱的高，r为球的半径，l≥2）．假设该储油罐的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为c千元，半球形部分每平方米建造费用为3千元．设该储油罐的建造费用为y千元．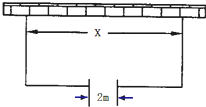
如图，围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的一扇门，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，一扇门的造价为600元，设利用的旧墙的长度为xm，总造价为y元．