题目内容
某班主任对全班50名学生进行了作业量多少的调查.数据如表:
(1)请完善上表中所缺的有关数据;
(2)试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系?
附:
K2=
.
| |
认为作业多 | 认为作业不多 | 合计 |
| 喜欢玩游戏 | 18 | 9 | |
| 不喜欢玩游戏 | 8 | 15 | |
| 合计 |
(2)试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系?
附:
| P(K2≥K0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:应用题,概率与统计
分析:(1)利用所给数据可得结论;
(2)根据表中所给的数据,代入求观测值的算式,求出观测值,把所求的观测值同临界值进行比较,得到喜欢玩电脑游戏与认为作业量的多少有关系的把握.
(2)根据表中所给的数据,代入求观测值的算式,求出观测值,把所求的观测值同临界值进行比较,得到喜欢玩电脑游戏与认为作业量的多少有关系的把握.
解答:
解:(1)
(2)将表中的数据代入公式得到K2=
的观测值
K=
≈5.059>5.024,
查表知P(K2≥5.024)=0.025,即说明在犯错误的概率不超过0.025的前提下认为喜欢玩游戏与作业量的多少有关系.
| 认为作业多 | 认为作业不多 | 合计 | |
| 喜欢玩游戏 | 18 | 9 | 27 |
| 不喜欢玩游戏 | 8 | 15 | 23 |
| 合计 | 26 | 24 | 50 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
K=
| 50×?18×15-8×9?2 |
| 26×24×27×23 |
查表知P(K2≥5.024)=0.025,即说明在犯错误的概率不超过0.025的前提下认为喜欢玩游戏与作业量的多少有关系.
点评:本题考查独立性检验的应用,本题解题的关键是理解临界值对应的概率的应用,能够正确的说出概率的意义.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
数列{an}中,a1,a2-a1,a3-a2,…,an-an-1…是首项为1、公比为
的等比数列,则an等于 ( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列不等关系成立的是( )
| A、sin31°>cos59° |
| B、-cos59°>-cos61° |
| C、tan31°>tan61° |
| D、sin59°>cos59° |
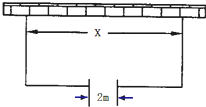 如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.
如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元. 把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右第j个数.
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右第j个数.