题目内容
在△ABC中，已知a=2
，b=
，A=130°，则此三角形（ ）
| 3 |
| 7 |
| 2 |
| A、无解 | B、只有一解 |
| C、有两解 | D、解的个数不确定 |
考点：正弦定理
专题：解三角形
分析：利用正弦定理和已知条件可求得sinB，通过A是钝角，推断B一定是锐角，则只能有一个解．
解答：
解：∵
=
，
∴sinB=
•sinA=
×sin130°=
sin130°＜
sin120°=
×
=
，
∴sinB有解，
∵A=130°＞
，
∴0＜B＜
，B只能有一个解．
故选B．
| a |
| sinA |
| b |
| sinB |
∴sinB=
| b |
| a |
| ||
2
|
| 7 | ||
4
|
| 7 | ||
4
|
| 7 | ||
4
|
| ||
| 2 |
| 7 |
| 8 |
∴sinB有解，
∵A=130°＞
| π |
| 2 |
∴0＜B＜
| π |
| 2 |
故选B．
点评：本题主要考查了正弦定理的应用．考查了学生推理和计算的能力．
练习册系列答案
天天向上口算本系列答案
相关题目
已知数列{an}满足a1=2，an+1=
，则a2014等于（ ）
| 1+an |
| 1-an |
| A、2 | ||
B、-
| ||
| C、-3 | ||
D、
|
等差数列的相邻4项分别是a+1，a+3，b，a+b，那么a，b的值依次为（ ）
| A、2，7 | B、1，6 |
| C、0，5 | D、无法确定 |
已知f（x）=ln（
-3x）+1，则f（lg3）+f（lg
）等于（ ）
| 1+9x2 |
| 1 |
| 3 |
| A、2 | B、1 | C、0 | D、-1 |
数列{an}中，a1，a2-a1，a3-a2，…，an-an-1…是首项为1、公比为
的等比数列，则an等于 （ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知等差数列{an}的前n项和为Sn，且满足S4+a25=5，则一定有（ ）
| A、a6是常数 |
| B、S7是常数 |
| C、a13是常数 |
| D、S13是常数 |
已知等比数列{an}，若a1+a2=20，a3+a4=80，则a5+a6等于（ ）
| A、480 | B、120 |
| C、240 | D、320 |
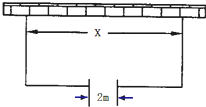如图，围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的一扇门，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，一扇门的造价为600元，设利用的旧墙的长度为xm，总造价为y元．