题目内容
给出以下四个命题:
①设p:a2+a≠0,q:a≠0,则p是q的充分不必要条件;
②过点(-1,2)且在x轴和y轴上的截距相等的直线方程是x+y-1=0;
③若函数y=f(x)与y=g(x)的图象关于直线y=x对称,则函数y=f(2x)与y=
g(x)的图象也关于直线y=x对称;
④若直线xsinα+ycosα+1=0和直线xcosα-
y-1=0垂直,则角α=kπ+或α=2kπ+
(k∈Z).
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
①设p:a2+a≠0,q:a≠0,则p是q的充分不必要条件;
②过点(-1,2)且在x轴和y轴上的截距相等的直线方程是x+y-1=0;
③若函数y=f(x)与y=g(x)的图象关于直线y=x对称,则函数y=f(2x)与y=
| 1 |
| 2 |
④若直线xsinα+ycosα+1=0和直线xcosα-
| 1 |
| 2 |
| π |
| 6 |
其中正确命题的序号为
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①a2+a≠0⇒a≠或-1,反过来不成立;由直线在坐标轴上的截距定义,可得②是假命题;根据函数y=f(x)与y=g(x)的图象关于直线y=x对称,可得③是真命题;根据两条直线垂直的充要条件,结合三角函数图象与性质,可得④是假命题.
解答:
解:对于①a2+a≠0⇒a≠0且-1,反过来不成立,∴p是q的充分不必要条件;
对于②,过点(-1,2)且在x轴和y轴上的截距相等的直线方程除了x+y-1=0还有y=-2x,故②不正确;
对于③,由题意,(a,b)满足y=f(x),则(b,a)满足y=g(x),∴(
,b)满足y=f(x),则(b,
)满足y=g(x),
∴函数y=f(2x)与y=
g(x)的图象也关于直线y=x对称,正确;
对于④,直线xsinα+ycosα+1=0和直线xcosα-
y-1=0垂直,则sinαcosα-
cosα=0,可得sinα=
或cosα=0,所以α=2kπ+
或α=2kπ+
或α=kπ+
(k∈Z),由此可得④不正确;
故答案为:①③
对于②,过点(-1,2)且在x轴和y轴上的截距相等的直线方程除了x+y-1=0还有y=-2x,故②不正确;
对于③,由题意,(a,b)满足y=f(x),则(b,a)满足y=g(x),∴(
| a |
| 2 |
| a |
| 2 |
∴函数y=f(2x)与y=
| 1 |
| 2 |
对于④,直线xsinα+ycosα+1=0和直线xcosα-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 2 |
故答案为:①③
点评:本题以命题真假的判断为载体,考查了充分不必要条件、两条直线位置关系和简单的三角方程等知识,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知
xdx=2(a>0),则a的值为( )
| ∫ | a 0 |
| A、1 | B、2 | C、3 | D、4 |
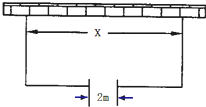 如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.
如图,围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的一扇门,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,一扇门的造价为600元,设利用的旧墙的长度为xm,总造价为y元.