题目内容
若直线kx-y-2=0与曲线
=|x|-1有两个不同的交点,则实数k的取值范围是 .
| 1-(y-1)2 |
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:将曲线
=|x|-1化简,可得它表示圆心分别为C1(1,1)、C2(-1,1),半径等于1的两个半圆;而kx-y-2=0表示经过定点A(0,-2)、斜率为k的直线.因此当直线与曲线有两个不同的交点时,直线与左边的半圆有两个交点,或与右边的半圆有两个交点.由此对图形加以观察,利用点到直线的距离公式和直线的斜率公式建立关于k的不等式组,解之即可得到实数k的取值范围.
| 1-(y-1)2 |
解答:
解:①当x≥0时,曲线
=|x|-1即
=x-1,
两边平方,整理得(x-1)2+(y-1)2=1,(x≥1)
表示以C1(1,1)为圆心,半径r1=1的圆的右半圆;
②当x<0时,曲线
=|x|-1即
=-x-1,
两边平方,整理得(x+1)2+(y-1)2=1,(x≤-1)
表示以C2(-1,1)为圆心,半径r2=1的圆的左半圆.
直线kx-y-2=0即y=kx-2,表示经过定点A(0,-2)、斜率为k的直线.
因此,直线kx-y-2=0与曲线
=|x|-1有两个不同的交点,
就是直线kx-y-2=0与两个半圆组成的图形有两个交点,
①当直线kx-y-2=0与右半圆C1有两个交点时,记点B(1,0),
可得直线到圆心的距离小于半径,且直线的斜率小于或等于AB的斜率,
∴
<1且k≤kAB=
=2,解之得
<k≤2;
②当直线kx-y-2=0与左半圆C2有两个交点时,类似于①的方程解得-2≤k<-
.
综上所述,实数k的取值范围是
<k≤2或-2≤k<-
,即k∈[-2,-
)∪(
,2].
故答案为:[-2,-
)∪(
,2]
| 1-(y-1)2 |
| 1-(y-1)2 |
两边平方,整理得(x-1)2+(y-1)2=1,(x≥1)
表示以C1(1,1)为圆心,半径r1=1的圆的右半圆;
②当x<0时,曲线
| 1-(y-1)2 |
| 1-(y-1)2 |

两边平方,整理得(x+1)2+(y-1)2=1,(x≤-1)
表示以C2(-1,1)为圆心,半径r2=1的圆的左半圆.
直线kx-y-2=0即y=kx-2,表示经过定点A(0,-2)、斜率为k的直线.
因此,直线kx-y-2=0与曲线
| 1-(y-1)2 |
就是直线kx-y-2=0与两个半圆组成的图形有两个交点,
①当直线kx-y-2=0与右半圆C1有两个交点时,记点B(1,0),
可得直线到圆心的距离小于半径,且直线的斜率小于或等于AB的斜率,
∴
| |k-2| | ||
|
| -2-0 |
| 0-1 |
| 4 |
| 3 |
②当直线kx-y-2=0与左半圆C2有两个交点时,类似于①的方程解得-2≤k<-
| 4 |
| 3 |
综上所述,实数k的取值范围是
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
故答案为:[-2,-
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题给出直线与曲线有两个交点,求参数k的取值范围.着重考查了圆的标准方程、点到直线的距离公式、直线的斜率公式和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x2-x,则当x∈[-1,0]时,f(x)的最小值为( )
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
已知函数f(x)=ax5+bx3+cx-2,且f (-12)=10,则f(12)=( )
| A、-14 | B、-12 |
| C、-10 | D、10 |
已知空间4个球,它们的半径均为2,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
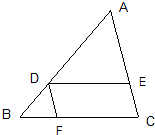 (几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=
(几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=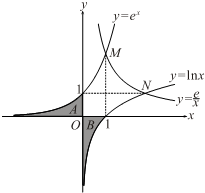 利用自然对数的底数e(e=2.71828…)构建三个基本初等函数
利用自然对数的底数e(e=2.71828…)构建三个基本初等函数