Question

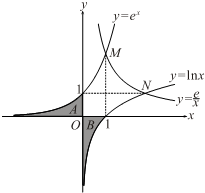利用自然对数的底数e（e=2.71828…）构建三个基本初等函数y=ex，y=lnx，y=

e

x

(x＞0)．探究发现，它们具有以下结论：三个函数的图象形成的图形（如图）具有“对称美”；图形中阴影区A的面积为1等．M，N是函数图象的交点．
（Ⅰ）根据图形回答下列问题：
①写出图形的一条对称轴方程；
②说出阴影区B的面积；
③写出M，N的坐标．
（Ⅱ）设f(x)=ex-lnx+

e

x

，证明：对任意的正实数x₁，x₂，都有

f(x1)+f(x2)

2

≥f(

x1+x2

2

)．

Answer 1

考点：指数函数综合题

专题：函数的性质及应用

分析：（Ⅰ）数形结合可得①三个函数的图象形成的图形的一条对称轴方程，再根据②阴影区A、B关于直线y=x对称，求得阴影区B的面积．以及③M、N的坐标．
（Ⅱ）先化简不等式的两边，再用作差比较法证得不等式成立．

解答： 解：（Ⅰ）∵y=

e

x

（x＞0）的图象是反比例函数y=

e

x

（x≠0）的图象位于第一象限内的一支，
∴y=

e

x

（x＞0）的图象关于直线y=x对称．
又y=e^x，y=lnx=log_ex互为反函数，它们的图象关于直线y=x互相对称，从而可知：
①三个函数的图象形成的图形的一条对称轴方程为y=x．
②阴影区A、B关于直线y=x对称，故阴影区B的面积为1．
③M（1，e），N（e，1）．（6分）
（Ⅱ）由于

f(x1)+f(x2)

2

=

ex1+ e x1 -lnx1+ex2+ e x2 -lnx2

2

=

ex1+ex2+ e x1 + e x2 -ln(x1x2)

2

，f(

x1+x2

2

)=e

x1+x2

2

+

e

x1+x2 2

-ln

x1+x2

2

=e

x1+x2

2

+

2e

x1+x2

-ln

x1+x2

2

，

f(x1)+f(x2)

2

-f(

x1+x2

2

)=

ex1+ex2+ e x1 + e x2 -ln(x1x2)

2

-e

x1+x2

2

-

2e

x1+x2

+ln

x1+x2

2

=

ex1+ex2

2

-e

x1+x2

2

+

e x1 + e x2

2

-

2e

x1+x2

+ln

x1+x2

2

-

ln(x1x2)

2

 
=

ex1+ex2-2 ex1+x2

2

+

(x1+x2)e

2x1x2

-

2e

x1+x2

+ln

x1+x2

2

-ln

x1x2

=

ex1+ex2-2 ex1•ex2

2

+

(x1+x2)2-4x1x2

2x1x2(x1+x2)

•e+ln

x1+x2

2

-ln

x1x2

 
=

( ex1 - ex2 )2

2

+

(x1-x2)2

2x1x2(x1+x2)

•e+ln

x1+x2

2

-ln

x1x2

．（*）
∵

x1+x2

2

-

x1x2

=

( x1 - x2 )2

2

≥0，
∴ln

x1+x2

2

≥ln

x1x2

，即ln

x1+x2

2

-ln

x1x2

≥0．
从而可知（*）≥0，即

f(x1)+f(x2)

2

≥f(

x1+x2

2

)对任意的正实数x₁，x₂都成立．

点评：本题主要考查指数函数、对数函数的图象和性质应用，用比较法证明不等式，属于中档题．