题目内容
实数m取什么值时,复数z=(m+1)+(m-2)i是:(1)实数?(2)虚数?(3)纯虚数?
考点:复数的基本概念
专题:数系的扩充和复数
分析:利用复数为实数、虚数、纯虚数的充要条件即可得出.
解答:
解:∵复数z=(m+1)+(m-2)i是:
(1)由m-2=0,解得m=2,∴m=2时,复数z是实数;
(2)由m-2≠0,解得m≠2,∴m≠2时,复数z是虚数;
(3)由
,解得m=-1,∴m=-1时,复数z是纯虚数.
(1)由m-2=0,解得m=2,∴m=2时,复数z是实数;
(2)由m-2≠0,解得m≠2,∴m≠2时,复数z是虚数;
(3)由
|
点评:本题考查了复数为实数、虚数、纯虚数的充要条件,属于基础题.

练习册系列答案
相关题目
已知复数z=
,则|z|=( )
1+
| ||
| 1-i |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
已知i是虚数单位,复数z=
,则|z-2|=( )
| 2i |
| 1+i |
| A、2 | ||
B、2
| ||
C、
| ||
| D、1 |
若非零实数a,b,c成等差数列,则函数y=ax2+bx+
c的图象与x轴交点的个数为( )
| 1 |
| 4 |
| A、0 | B、1 | C、2 | D、1或2 |
数列0,
,
,
,
,…的通项公式为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|

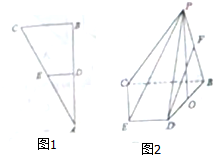 如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.
如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.