题目内容
数列0,
,
,
,
,…的通项公式为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:数列0,
,
,
,
,…即
,
,
,
,
,…,即可得出通项公式.
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
| 1-1 |
| 1+1 |
| 2-1 |
| 2+1 |
| 3-1 |
| 3+1 |
| 4-1 |
| 4+1 |
| 5-1 |
| 5+1 |
解答:
解:数列0,
,
,
,
,…即
,
,
,
,
,…,
因此其通项公式为an=
.
故选:C.
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
| 1-1 |
| 1+1 |
| 2-1 |
| 2+1 |
| 3-1 |
| 3+1 |
| 4-1 |
| 4+1 |
| 5-1 |
| 5+1 |
因此其通项公式为an=
| n-1 |
| n+1 |
故选:C.
点评:本题考查了通项公式的求法,考查了观察分析猜想归纳能力,属于基础题.

练习册系列答案
相关题目
在等比数例{an}中,2a4,a6,48成等差数列,且a3•a5=64,则{an}的前8项和为( )
| A、255 | B、85 |
| C、255或-85 | D、255或85 |
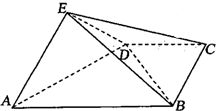 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.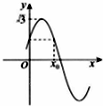 已知f(x)=Asin(2x+
已知f(x)=Asin(2x+