题目内容
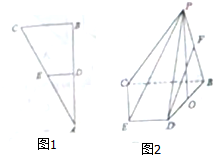 如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.
如图1所示,在△ABC中,∠B=90°,D,E分别是AB,AC的中点,将△ADE沿DE折到△PDE的位置,使得∠PDB=60°,如图2所示,连接PB,PC,CD,O,F分别是BD,PB的中点,连接PO,DF,PC.(1)求证:PO⊥平面BCED;
(2)求证:DF∥平面PCE;
(3)若DB=2,BC=
| 2 |
考点:二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得AB⊥BC且DE∥BC,DE⊥AB,DE⊥PD,从而DE⊥平面PDB,进而DE⊥PO,又PD=BD,O是BD中点,从而PO⊥BD,由此能证明PO⊥平面BCDE.
(2)取BC中点M,连结MF、MD,由此推导出平面PCF∥平面FMD,从而能证明DF∥平面PCE.
(3)以O为原点,OB为y轴,OP为z轴,建立空间直角坐标系,求出平面FCD的法向量和平面BCD的法向量,利用向量法能求出二面角F-CD-B的大小.
(2)取BC中点M,连结MF、MD,由此推导出平面PCF∥平面FMD,从而能证明DF∥平面PCE.
(3)以O为原点,OB为y轴,OP为z轴,建立空间直角坐标系,求出平面FCD的法向量和平面BCD的法向量,利用向量法能求出二面角F-CD-B的大小.
解答:
(1)证明:∵在△ABC中,∠B=90°,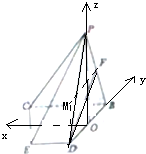
D,E分别是AB,AC的中点,
∴AB⊥BC且DE∥BC,∴DE⊥AB,∴DE⊥PD,
又DE⊥BD,∴DE⊥平面PDB,又PO?平面PDB,
∴DE⊥PO,又PD=BD,O是BD中点,∴PO⊥BD,
∴PO⊥平面BCDE.
(2)证明:取BC中点M,连结MF、MD,
∵F是BD中点,DE
BC,∴MF∥PC,DE∥EC,
∵FM∩DM=M,∴平面PCF∥平面FMD,
又DF?平面PCE,∴DF∥平面PCE.
(3)解:以O为原点,OB为y轴,OP为z轴,建立空间直角坐标系,
P(0,0,
),B(0,1,0),F(0,
,
),C(
,0,0),D(0,-1,0),
=(-
,-1,0),
=(-
,
,
),
=(-
,1,0),
设平面FCD的法向量为
=(x,y,z),
则
,取x=1,得
=(1,-
,
),
平面BCD的法向量为
=(0,0,1),
设二面角F-CD-B的大小为θ,
cosθ=
=
=
.
∴二面角F-CD-B的大小为arccos
.

D,E分别是AB,AC的中点,
∴AB⊥BC且DE∥BC,∴DE⊥AB,∴DE⊥PD,
又DE⊥BD,∴DE⊥平面PDB,又PO?平面PDB,
∴DE⊥PO,又PD=BD,O是BD中点,∴PO⊥BD,
∴PO⊥平面BCDE.
(2)证明:取BC中点M,连结MF、MD,
∵F是BD中点,DE
| ∥ |
. |
| 1 |
| 2 |
∵FM∩DM=M,∴平面PCF∥平面FMD,
又DF?平面PCE,∴DF∥平面PCE.
(3)解:以O为原点,OB为y轴,OP为z轴,建立空间直角坐标系,
P(0,0,
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| CD |
| 2 |
| CF |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| CB |
| 2 |
设平面FCD的法向量为
| n |
则
|
| n |
| 2 |
| ||
| 3 |
平面BCD的法向量为
| m |
设二面角F-CD-B的大小为θ,
cosθ=
|
| ||||
|
|
| ||||
|
| ||
| 11 |
∴二面角F-CD-B的大小为arccos
| ||
| 11 |
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

练习册系列答案
相关题目
已知函数f(x)=log3(10x+
-2),则f(x)的值域为( )
| 1 |
| 10x |
| A、(-∞,-3) |
| B、(-3,3) |
| C、[0,+∞) |
| D、(-∞,+∞) |
已知全集U=R,集合A={x||x-1|≤2},CUB=(-∞,1)∪[4,+∞),则A∪B=( )
| A、[1,3] |
| B、(1,3] |
| C、[-1,4] |
| D、[-1,4) |
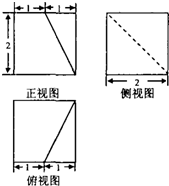
若某几何体的三视图如图所示,则此几何体的体积是( )

A、
| ||
B、
| ||
| C、7 | ||
| D、6 |
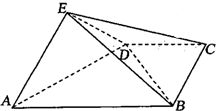 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,AB=4,BC=CD=EA=ED=2,F是线段EB的中点.