题目内容
（文科）不等式|x|-1≤0的解集为（ ）
| A、（-∞，1] |
| B、[-1，1] |
| C、（-∞，0] |
| D、[0，1] |
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由|x|-1≤0可得|x|≤1，从而可得答案．
解答：
解：∵|x|-1≤0，
∴|x|≤1，
解得-1≤x≤1．
故选：B．
∴|x|≤1，
解得-1≤x≤1．
故选：B．
点评：本题考查绝对值不等式的解法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若某班有4个小组各从3处风景点中选一处进行旅游观光，则不同选择方案的种数为（ ）
| A、4种 | B、24种 |
| C、64种 | D、81种 |
在空间四边形ABCD中，已知AB=3，BC=2
，CD=4，AD=
，BD=2，则异面直线AC与BD所成角的大小是（ ）
| 5 |
| 5 |
| A、30° | B、45° |
| C、60° | D、90° |
函数y=sin2x+2cosx在区间[-
，a]上的值域为[-
，2]，则a的范围是（ ）
| 2π |
| 3 |
| 1 |
| 4 |
A、[-
| ||||
B、（-
| ||||
C、[0，
| ||||
D、（0，
|
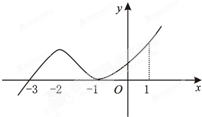如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：①-3数y=f（x）的极值点；
②-1函数y=f（x）的最小值；
③y=f（x）在x=0处切线的斜率小于零；
④y=f（x）在区间（-3，1）上单调递增．
则正确命题的序号是（ ）
| A、①② | B、①④ | C、②③ | D、③④ |
若a=
x2dx，b=
exdx，c=
sinxdx，则a、b、c大小关系是（ ）
| ∫ | 2 0 |
| ∫ | 2 0 |
| ∫ | 2 0 |
| A、c＜a＜b |
| B、a＜c＜b |
| C、a＜b＜c |
| D、c＜b＜a |
过点P（1，3）的动直线l与圆x2+y2=3交于不同两点、B，在线段AB上取一点Q，满足
=-λ
，
=λ
，λ≠0且λ≠±1，则点Q所在的直线的方程为（ ）
| AP |
| PB |
| AQ |
| QB |
| A、x-3y=3 |
| B、x-y=3 |
| C、x+y=3 |
| D、x+3y=3 |
下列命题是真命题的是（ ）
| A、?x∈R，x＞0 |
| B、?x∈R，x02+2x0+3=0 |
| C、有的三角形是正三角形 |
| D、每一个四边形都有外接圆 |
sin（
+α）=
，则cos（
-α）的值为（ ）
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|