题目内容
在空间四边形ABCD中,已知AB=3,BC=2
,CD=4,AD=
,BD=2,则异面直线AC与BD所成角的大小是( )
| 5 |
| 5 |
| A、30° | B、45° |
| C、60° | D、90° |
考点:异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:根据已知的边的关系可以判断△ABD,和△BCD为Rt△,所以得到BD⊥AD,BD⊥CD,所以BD⊥平面ACD,所以BD⊥AC,所以异面直线AC与BD所成角的大小就求出来了.
解答:
解:如图,∵AD=
,BD=2,AB=3,∴AB2=AD2+BD2;
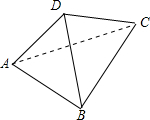 ∴△ABD为Rt△,∠ADB=90°,即BD⊥AD,同理,BD⊥CD,AD∩CD=D;
∴△ABD为Rt△,∠ADB=90°,即BD⊥AD,同理,BD⊥CD,AD∩CD=D;
∴BD⊥平面ACD,AC?平面ACD;
∴BD⊥AC,∴异面直线AC与BD所成角的大小是90°.
故选:D.
| 5 |
 ∴△ABD为Rt△,∠ADB=90°,即BD⊥AD,同理,BD⊥CD,AD∩CD=D;
∴△ABD为Rt△,∠ADB=90°,即BD⊥AD,同理,BD⊥CD,AD∩CD=D;∴BD⊥平面ACD,AC?平面ACD;
∴BD⊥AC,∴异面直线AC与BD所成角的大小是90°.
故选:D.
点评:考查根据边的关系判断直角三角形的方法,线面垂直的判定定理,及线面垂直的性质,异面直线所成的角.

练习册系列答案
相关题目
复数(1+3i)•i的虚部是( )
| A、0 | B、1 | C、3 | D、-2 |
在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( )
| A、残差 |
| B、残差平方和 |
| C、随机误差 |
| D、相关指数R2 |
利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定分类变量“X和Y有关系”的可信度.如果K2的观测值为7.8,则下列说法中正确的是( )
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A、在犯错误的概率不超过1%的前提下,认为“X和Y有关系” |
| B、在犯错误的概率不超过1%的前提下,认为“X和Y有关系” |
| C、有99.5%以上的把握认为“X和Y有关系” |
| D、有99.5%以上的把握认为“X和Y有关系” |
要得到函数y=
cosx的图象,需将函数y=
sin(2x+
)的图象上所有的点的变化正确的是( )
| 2 |
| 2 |
| π |
| 4 |
A、横坐标缩短到原来的
| ||||
B、横坐标缩短到原来的
| ||||
C、横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动
| ||||
D、横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动
|
在(
+
)100的展开式中,有理项的个数是( )
| 2 |
| 3 | 5 |
| A、15个 | B、33个 |
| C、17个 | D、16个 |
(文科)不等式|x|-1≤0的解集为( )
| A、(-∞,1] |
| B、[-1,1] |
| C、(-∞,0] |
| D、[0,1] |
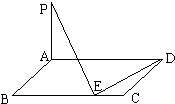 如图:已知矩形ABCD中,AB=2,BC=a,若PA⊥面AC,在BC边上取点E,使PE⊥DE,则满足条件的E点有两个时,a的取值范围是( )
如图:已知矩形ABCD中,AB=2,BC=a,若PA⊥面AC,在BC边上取点E,使PE⊥DE,则满足条件的E点有两个时,a的取值范围是( )| A、a>4 | B、a≥4 |
| C、0<a<4 | D、0<a≤4 |