题目内容
下列命题是真命题的是（ ）
| A、?x∈R，x＞0 |
| B、?x∈R，x02+2x0+3=0 |
| C、有的三角形是正三角形 |
| D、每一个四边形都有外接圆 |
考点：特称命题,全称命题
专题：简易逻辑
分析：直接利用全称命题以及特称命题命题的真假判断即可．
解答：
解：?x∈R，x＞0显然不正确；?x∈R，x02+2x0+3=0，因为△＜0，所以方程无解，命题不正确；
有的三角形是正三角形，显然正确；每一个四边形都有外接圆，显然不正确；
故选：C．
有的三角形是正三角形，显然正确；每一个四边形都有外接圆，显然不正确；
故选：C．
点评：本题考查命题的真假的判断，基本知识的考查．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
在回归分析中，代表了数据点和它在回归直线上相应位置的差异的是（ ）
| A、残差 |
| B、残差平方和 |
| C、随机误差 |
| D、相关指数R2 |
（文科）不等式|x|-1≤0的解集为（ ）
| A、（-∞，1] |
| B、[-1，1] |
| C、（-∞，0] |
| D、[0，1] |
已知x∈R，P=ex+e-x，Q=（sinx+cosx）2，下面的关系式一定成立的是（ ）
| A、?x0∈R，使P=Q |
| B、P＞Q |
| C、P≤Q |
| D、P＜Q |
已知向量
=（2cosα，2sinα），
=（2sinβ，2cosβ），|
+
|=
，则sin（α+β）的值为（ ）
| m |
| n |
| m |
| n |
8
| ||
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知平面上不共线的四点O，A，B，C，若
-4
+3
=0，则
=（ ）
| OA |
| OB |
| OC |
|
| ||
|
|
| A、3 | B、4 | C、5 | D、6 |
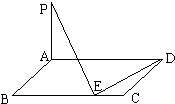如图：已知矩形ABCD中，AB=2，BC=a，若PA⊥面AC，在BC边上取点E，使PE⊥DE，则满足条件的E点有两个时，a的取值范围是（ ）| A、a＞4 | B、a≥4 |
| C、0＜a＜4 | D、0＜a≤4 |
（1
）0-（1-0.5-2）÷(
)
的值为（ ）
| 1 |
| 2 |
| 27 |
| 8 |
| 2 |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
