题目内容
用反证法证明结论“?x0∈R”使得P（x0）成立，应假设（ ）
| A、?x0∈R，使得P（x0）不成立 |
| B、?x∈R，P（x）均成立 |
| C、?x∈R，P（x）均不成立 |
| D、不存在x0∈R，使得P（x0）不成立 |
考点：反证法与放缩法
专题：不等式
分析：根据反证法的步骤，假设是对原命题结论的否定，即可得出正确选项．
解答：
解：根据反证法的步骤，假设是对原命题结论的否定，P（x0）成立的否定是使得P（x0）不成立，
故选：A
故选：A
点评：本题考查反证法的概念，逻辑用语，否命题与命题的否定的概念，逻辑词语的否定．
练习册系列答案
53随堂测系列答案
相关题目
设{an}是首项为-
，公差为d（d≠0）的等差数列，Sn为其前n项和，若S1，S2，S4成等比数列，则d=（ ）
| 1 |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
D、
|
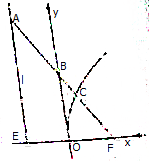如图，过抛物线y2=2px（p＞0）的焦点F的直线分别交抛物线的准线l、y轴、抛物线于A、B、C三点，若| AB |
| BC |
A、-
| ||||
B、-
| ||||
C、-
| ||||
| D、-1 |
设a＞0且a≠1，则“函数f（x）=ax在R上是减函数”，是“函数g（x）=（2-a）x3在R上是增函数”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |