题目内容
已知f(x)=logax,其反函数为g(x).
(1)解关于x的方程f(x-1)=f(a-x)-f(5-x);
(2)设F(x)=(2m-1)g(x)+(
-
)g(-x),若F(x)有最小值,试求其表达式h(m);
(3)求h(m)的最大值.
(1)解关于x的方程f(x-1)=f(a-x)-f(5-x);
(2)设F(x)=(2m-1)g(x)+(
| 1 |
| m |
| 1 |
| 2 |
(3)求h(m)的最大值.
考点:反函数,指数函数的图像与性质
专题:函数的性质及应用
分析:(1)根据函数式子得出∴
,
(2)得出h(m)=2
,
<m<2,运用基本不等式求解即可,
(3)化简得出h(m)=2
=2
,
<m<2
利用m+
≥2(m=1时等号成立)即可得出答案.
|
(2)得出h(m)=2
(2m-1)(
|
| 1 |
| 2 |
(3)化简得出h(m)=2
(2m-1)(
|
|
| 1 |
| 2 |
利用m+
| 1 |
| m |
解答:
解;f(x)=logax,其反函数为g(x)=ax,
(1)∵f(x-1)=f(a-x)-f(5-x);
∴loga(x-1)=loga(a-x)-loga(5-x),
∴
,
∵x2-7x+5+a=0,
∴x=
,
∵x>1,x<5,x<a,
∴x=
,
(2)∵设F(x)=(2m-1)g(x)+(
-
)g(-x),
∴设F(x)=(2m-1)ax+(
-
)a-x,
设F(x)=(2m-1)g(x)+(
-
)g(-x),
∴h(m)=2
,
<m<2,
(3)h(m)=2
=2
,
<m<2,
∵m+
≥2(m=1时等号成立)
∴
-(m+
)≤
-2=
,
∴h(m)的最大值为2
=
.
(1)∵f(x-1)=f(a-x)-f(5-x);
∴loga(x-1)=loga(a-x)-loga(5-x),
∴
|
∵x2-7x+5+a=0,
∴x=
7±
| ||
| 2 |
∵x>1,x<5,x<a,
∴x=
7±
| ||
| 2 |
(2)∵设F(x)=(2m-1)g(x)+(
| 1 |
| m |
| 1 |
| 2 |
∴设F(x)=(2m-1)ax+(
| 1 |
| m |
| 1 |
| 2 |
设F(x)=(2m-1)g(x)+(
| 1 |
| m |
| 1 |
| 2 |
∴h(m)=2
(2m-1)(
|
| 1 |
| 2 |
(3)h(m)=2
(2m-1)(
|
|
| 1 |
| 2 |
∵m+
| 1 |
| m |
∴
| 5 |
| 2 |
| 1 |
| m |
| 5 |
| 2 |
| 1 |
| 2 |
∴h(m)的最大值为2
|
| 2 |
点评:本题考综合考查了函数的性质,运算,结合基本不等式求解,属于中档题,关键是运算化简,考查了计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设全集U=Z,集合M={1,2},P={-2,-1,0,1,2},则P∩∁UM=( )
| A、{0} | B、{1} |
| C、{-1,-2,0} | D、∅ |
已知三角函数f(x)=Asin(ωx+φ)+b同时满足以下三个条件:
①定义域为R;
②对任意实数x都有f(x)≤f(3);
③f(x+2)=
+
,
则f(x)的单调区间为( )
①定义域为R;
②对任意实数x都有f(x)≤f(3);
③f(x+2)=
| 1 |
| 2 |
| f(x)-f2(x) |
则f(x)的单调区间为( )
| A、[4k-1,4k+3],k∈Z |
| B、[4k+1,4k+3],k∈Z |
| C、[8k-2,8k+2],k∈Z |
| D、[8k+2,8k+6],k∈Z |
用反证法证明结论“?x0∈R”使得P(x0)成立,应假设( )
| A、?x0∈R,使得P(x0)不成立 |
| B、?x∈R,P(x)均成立 |
| C、?x∈R,P(x)均不成立 |
| D、不存在x0∈R,使得P(x0)不成立 |
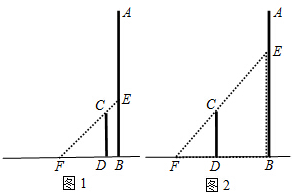 如图所示,直立在地面上的两根钢管AB和CD,AB=10
如图所示,直立在地面上的两根钢管AB和CD,AB=10