题目内容
已知函数f（x）=
，则函数f（x+1）的定义域为（ ）
| 2-|x| |
| A、[0，2] |
| B、[-1，2] |
| C、[-1，3] |
| D、[-3，1] |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：求出f（x）的定义域，再由x+1在f（x）的定义域内求解x的集合得答案．
解答：
解：∵数f（x）=
，
由2-|x|≥0，得-2≤x≤2．
∴f（x）的定义域为[-2，2]．
由-2≤x+1≤2，得-3≤x≤1．
∴函数f（x+1）的定义域为[-3，1]．
故选：D．
| 2-|x| |
由2-|x|≥0，得-2≤x≤2．
∴f（x）的定义域为[-2，2]．
由-2≤x+1≤2，得-3≤x≤1．
∴函数f（x+1）的定义域为[-3，1]．
故选：D．
点评：本题考查了函数的定义域及其求法，关键是对该类问题求解的理解，是基础题．
练习册系列答案
相关题目
函数f（x）=
sin2x最小值是（ ）
| 1 |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
已知实数集合M={x|
+
=1}，N={y|y=sinx，x∈M}，则M∩N=（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、[-3，3] |
| B、[-1，1] |
| C、（-1，1） |
| D、[-sin3，sin3] |
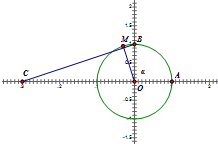如图，A、B是单位圆与x轴、y轴正半轴的交点，点M在单位圆上，∠AOM=α（0＜α＜π），点C（-3，0），若BC⊥OM，则sin（2α-| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将参加冬季越野跑的600名选手编号为：001，002…，600．采用系统抽样方法抽取一个容量为50的样本，把编号分50组后，在第一组的001至012这12个编号中随机抽得的号码为004，这600名选手分穿着三种颜色的衣服，001到301穿红色衣服，从302到496穿白色衣服，从497到600穿黄色衣服，若从样本中任意抽取一个，则抽到穿黄色衣服的选手概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
一个不透明的盒子里有质地、大小完全相同的5个球，编号分别为1，2，3，4，5，甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，如果两个编号的和为偶数算甲赢，否则算乙赢．那么甲赢的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、以上均不对 |
等比数列{an}中，a3、a15是方程x2-6x+8=0的两根，则a1a9a17=（ ）
A、16
| ||||
B、-16
| ||||
C、16
| ||||
| D、64 |
若函数f（x）=sin2x-cos2x+sin2x-m在[0，
]上有零点，则实数m的取值范围为（ ）
| π |
| 4 |
A、[-1，
| ||
| B、[-1，1] | ||
C、[1，
| ||
D、[-
|
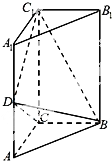如图，三棱柱ABC-A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=2，BC=4，AA1=4，D是棱AA1的中点．