题目内容
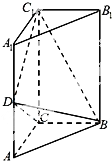 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=2,BC=4,AA1=4,D是棱AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=2,BC=4,AA1=4,D是棱AA1的中点.(1)证明:平面BDC1⊥平面BDC;
(2)求三棱锥C1-BCD外接球与三棱柱ABC-A1B1C1外接球的体积之比.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知得BC⊥AC,又侧面垂直底面,BC⊥侧面A1ACC1,从而C1D⊥BC,由此能证明平面BDC1⊥平面BDC.
(2)由(1)知,∠C1DB=90°,∠C1CB=90°,C1B是三棱锥C1-BCD外接球的直径,且C1B=4
,AB1是三棱柱ABC-A1B1C1外接球的直径,且AB1=6,由此能求出三棱锥C1-BCD外接球与三棱柱ABC-A1B1C1外接球的体积之比.
(2)由(1)知,∠C1DB=90°,∠C1CB=90°,C1B是三棱锥C1-BCD外接球的直径,且C1B=4
| 2 |
解答:
(1)证明:底面ACB中,∠ACB=90°,
∴BC⊥AC,又侧面垂直底面,
则BC⊥侧面A1ACC1,C1D?侧面A1ACC1,则C1D⊥BC,
侧面A1ACC1中,AD=AC=2,∴CD=2
,
又CC1=4,∴C1C2=C1D2+CD2,∴C1D⊥CD,
则C1D⊥面BCD,C1D?平面BDC1,
∴平面BDC1⊥平面BDC.
(2)解:由(1)知,∠C1DB=90°,∠C1CB=90°,
∴C1B是三棱锥C1-BCD外接球的直径,且C1B=4
,
由题意得AB1是三棱柱ABC-A1B1C1外接球的直径,且AB1=6,
∴三棱锥C1-BCD外接球与三棱柱ABC-A1B1C1外接球的体积之比为:
=(
)3=
.
∴BC⊥AC,又侧面垂直底面,
则BC⊥侧面A1ACC1,C1D?侧面A1ACC1,则C1D⊥BC,
侧面A1ACC1中,AD=AC=2,∴CD=2
| 2 |
又CC1=4,∴C1C2=C1D2+CD2,∴C1D⊥CD,
则C1D⊥面BCD,C1D?平面BDC1,
∴平面BDC1⊥平面BDC.
(2)解:由(1)知,∠C1DB=90°,∠C1CB=90°,
∴C1B是三棱锥C1-BCD外接球的直径,且C1B=4
| 2 |
由题意得AB1是三棱柱ABC-A1B1C1外接球的直径,且AB1=6,
∴三棱锥C1-BCD外接球与三棱柱ABC-A1B1C1外接球的体积之比为:
| V1 |
| V2 |
4
| ||
| 6 |
16
| ||
| 27 |
点评:本题考查平面BDC1⊥平面BDC的证明,考查三棱锥C1-BCD外接球与三棱柱ABC-A1B1C1外接球的体积之比的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,则函数f(x+1)的定义域为( )
| 2-|x| |
| A、[0,2] |
| B、[-1,2] |
| C、[-1,3] |
| D、[-3,1] |
若向量
=(1,1),
=(1,-1),
=(-2,1),则
等于( )
| a |
| b |
| c |
| c |
A、-
| ||||||||
B、-
| ||||||||
C、-
| ||||||||
D、-
|
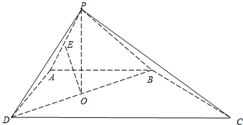 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点. 如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.
如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.